オイラーの式は
$\displaystyle P_c = n\frac{\pi^2 EI}{ l^2}$
と表せ、柱の境界条件が固定・自由端であるため、ｎは0.25となる。
また、断面二次モーメント
$I= \frac{bh^3}{ 12}$
を代入して整理すると
$\displaystyle P_c = \frac{\pi^2 ×200×10^9× \frac{(40×10^{-3})^4}{ 12}}{ 4 ×2^2}=26.3[kN]$
[解答]⑤
参考
座 屈
オイラーの公式によって熱応力によって発生する座屈を求める（H26）
オイラーの公式を用いた座屈荷重の算出（H25）
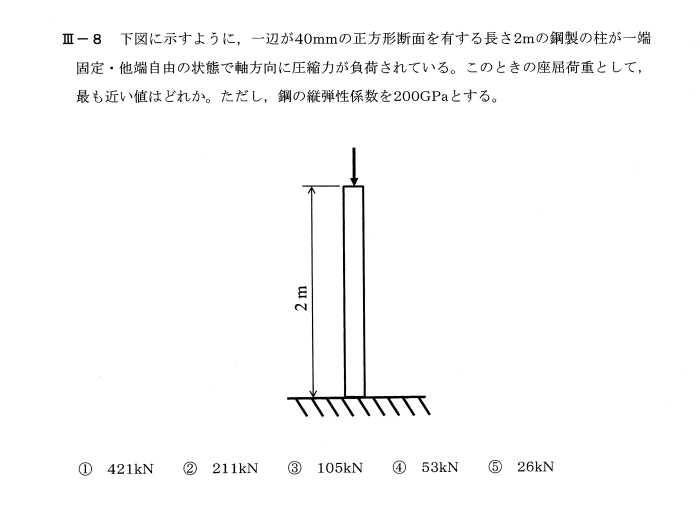
令和3年度技術士第一次試験問題［機械部門］ 専門科目Ⅲ-8 固定ｰ自由端の座屈荷重の算出
オイラーの式は
$\displaystyle P_c = n\frac{\pi^2 EI}{ l^2}$
と表せ、柱の境界条件が固定・自由端であるため、ｎは0.25となる。
また、断面二次モーメント
$I= \frac{bh^3}{ 12}$
を代入して整理すると
$\displaystyle P_c = \frac{\pi^2 ×200×10^9× \frac{(40×10^{-3})^4}{ 12}}{ 4 ×2^2}=26.3[kN]$
[解答]⑤
参考
座 屈
オイラーの公式によって熱応力によって発生する座屈を求める（H26）
オイラーの公式を用いた座屈荷重の算出（H25）
