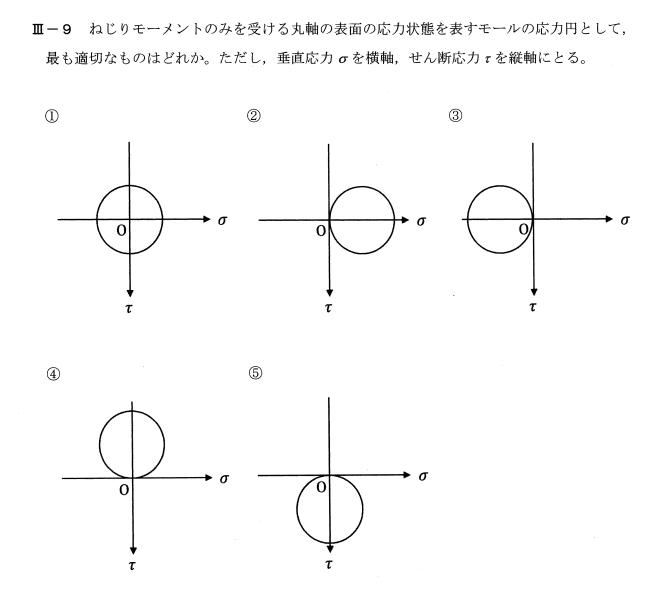
モールの応力円は下記式となる。
$(σ_x^{ ’ }-\frac{σ_x＋σ_y}{ 2 })^{ 2 }+τ^{ 2 }_{x^{ ’ }y^{ ’ }}=\frac{ 1 }{ 4 }(σ_x-σ_y)^{2}++τ^{ 2 }_{xy}$
ねじりの場合、せん断応力のみが作用する事（σ成分が0）を考慮すると、原点を中心とした円となる。
[解答]①
参考
ねじりモーメントを受ける丸棒のモールの応力円
第6回 モールの応力円
副業の始め方・おすすめ副業を紹介
僕が副業で毎月何万円も稼いでいるヒミツを メール読者さん限定で公開しています。
なぜ、時間がないサラリーマンでも 毎月何万円も稼ぐことが出来るのか？
100万円以上投資して得たスキルと実践で得たテクニックを 超初心者の方でもすぐに実践出来るよう噛み砕いて解説しています。
僕からのメールを何通か読み終わるころには、あなたも、 副業で稼ぐことができるヒミツが理解できるようになるはずです。
これから副業を始めようかなという人はもちろん 既に本格的に始めているあなたも大歓迎です！ 読者皆さんが様々な事で、個人で稼げる能力をつける事が出来たら嬉しいですね。
モールの応力円は下記式となる。
$(σ_x^{ ’ }-\frac{σ_x＋σ_y}{ 2 })^{ 2 }+τ^{ 2 }_{x^{ ’ }y^{ ’ }}=\frac{ 1 }{ 4 }(σ_x-σ_y)^{2}++τ^{ 2 }_{xy}$
ねじりの場合、せん断応力のみが作用する事（σ成分が0）を考慮すると、原点を中心とした円となる。
[解答]①
参考
ねじりモーメントを受ける丸棒のモールの応力円
第6回 モールの応力円
