以下に，熱応力問題の
丁寧な解説を書きます。
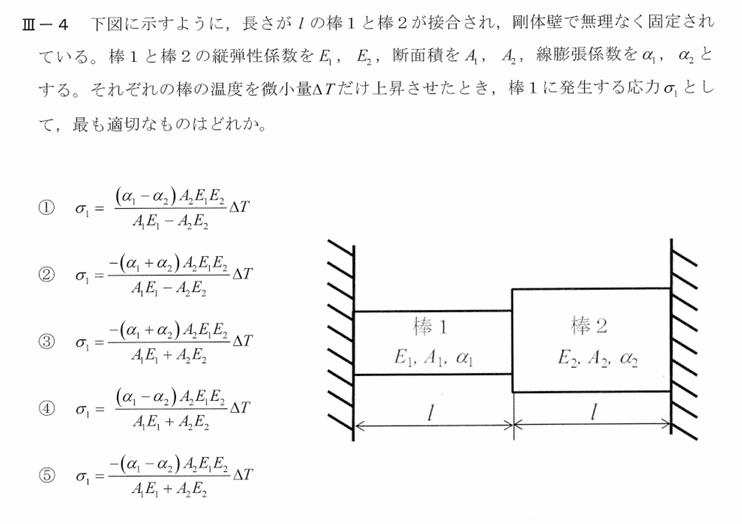
✅ 問題の状況整理
棒1と棒2（各長さ (l) ）が剛壁の間でつながれて固定されている。
両方の棒の温度を同じだけ (\Delta T) 上昇させる。
各パラメータ
|
ヤング率 |
断面積 |
線膨張係数 |
| 棒1 |
(E_1) |
(A_1) |
(\alpha_1) |
| 棒2 |
(E_2) |
(A_2) |
(\alpha_2) |
✅ 自由に膨張できるなら
棒1の自由熱膨張：
[
l\alpha_1\Delta T
]
棒2の自由熱膨張：
[
l\alpha_2\Delta T
]
しかし剛壁と互いに押し合うので
膨張できず，圧縮応力が発生。
✅ 伸び量と力の関係
熱膨張と力による変形を合わせて考える
[
\Delta l_1 = l\alpha_1\Delta T - \frac{P,l}{A_1E_1}
]
[
\Delta l_2 = l\alpha_2\Delta T - \frac{P,l}{A_2E_2}
]
ここで (P) は棒を押し縮める軸力（圧縮）
剛壁固定なので
[
\Delta l_1 + \Delta l_2 = 0
]
✅ 式をまとめる
[
l\alpha_1\Delta T - \frac{P,l}{A_1E_1}
- l\alpha_2\Delta T - \frac{P,l}{A_2E_2} = 0
]
両辺を (l) で割る：
[
\alpha_1\Delta T + \alpha_2\Delta T
- P\left(\frac{1}{A_1E_1} + \frac{1}{A_2E_2}\right)=0
]
(P) について解く
[
P
= \frac{(\alpha_1+\alpha_2)\Delta T}{\frac{1}{A_1E_1}+\frac{1}{A_2E_2}}
]
通分して
[
P = \frac{(\alpha_1+\alpha_2)A_1A_2E_1E_2}{A_1E_1+A_2E_2}\Delta T
]
✅ 棒1の応力
[
\sigma_1 = \frac{P}{A_1}
= \frac{(\alpha_1+\alpha_2)A_2E_1E_2}{A_1E_1+A_2E_2}\Delta T
]
圧縮なので負符号がつく：
[
\sigma_1 = -\frac{(\alpha_1+\alpha_2)A_2E_1E_2}{A_1E_1+A_2E_2}\Delta T
]
🎯 正しい選択肢
[
\boxed{③}
]
✅ 物理的な意味
- 棒1・棒2は直列バネの関係
- 熱膨張しようとするが壁で拘束 → 圧縮応力発生
- 硬くて断面積が大きい棒ほど（(E), (A) 大）力を多く負担
📝 ポイントまとめ
| 覚えるべき式 |
意味 |
| (\Delta l = \alpha \Delta T l + \frac{Pl}{AE}) |
熱＋力の変形 |
| (\Delta l_1 + \Delta l_2 = 0) |
壁固定で全体の伸び=0 |
| (\sigma = P/A) |
応力 |
必要なら，
数値を入れた例や
バネモデルの図解も作ります。
他の類題も解説できますので言ってくださいね。
[解答] ③
参考
剛体壁に固定された異材棒における温度上昇時の熱応力解析
平成27年度技術士第一次試験問題［機械部門］ 専門科目Ⅲ-4 温度上昇と熱応力
平成25年度技術士第一次試験問題［機械部門］ 専門科目Ⅲ-2 材料力学 固定された丸棒に生じる熱応力
