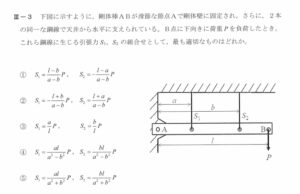
---

条件

1. モーメントのつり合い（A点周り）： $$P l = S_1 a + S_2 b$$ 
2. 変位と張力の関係（変位比と張力比が比例する）： $$\lambda_1 : \lambda_2 = S_1 : S_2 = a : b$$よって： $$S_1 = \frac{a}{b} S_2$$ 

計算

モーメントの式に $S_1 = \frac{a}{b} S_2$ を代入すると： $$P l = \frac{a}{b} S_2 \cdot a + S_2 \cdot b$$ $$P l = \frac{a^2}{b} S_2 + b S_2$$ $$P l = S_2 \left(\frac{a^2}{b} + b\right)$$ $$P l = S_2 \frac{a^2 + b^2}{b}$$ $$S_2 = \frac{P l \cdot b}{a^2 + b^2}$$   S1を計算すると $$S_1 = \frac{a}{b} S_2 = \frac{a}{b} \cdot \frac{P l \cdot b}{a^2 + b^2}$$ $$S_1 = \frac{P l \cdot a}{a^2 + b^2}$$   鋼線にかかる張力は以下の通りです： $$S_1 = \frac{P l \cdot a}{a^2 + b^2}, \quad S_2 = \frac{P l \cdot b}{a^2 + b^2}$$   [解答] ⑤ 参考：技術士第一次試験－令和2年度機械部門Ⅲ-3解答例 | 技術士のたまご

モーメントのつり合いと、力のつり合いではもとめられないですか？

結論：モーメントつり合い＋力つり合いだけでは求まりません。

なぜ?

未知量は

• 鋼線の張力 (S_1,S_2)（2つ）
• 支点Aの鉛直反力 (A_y)（1つ）

の計3つです。 静力学の式は [ \begin{aligned} &\text{鉛直力つり合い: } A_y+S_1+S_2=P \ &\text{Aまわりモーメント: } S_1 a+S_2 b=P l \end{aligned} ] の2本しかないため，このままでは未知数が1つ多く不静定です。 （水平力は0で自明。） そこで，変形の適合条件（剛体回転 ⇒ 伸び比 (\delta_1:\delta_2=a:b)）を使い， 同一鋼線より (S_1:S_2=a:b) を与えて初めて [ S_1=\frac{al}{a^2+b^2}P,\qquad S_2=\frac{bl}{a^2+b^2}P ] が一意に決まります（選択肢⑤）。

よくある誤り

Aの鉛直反力 (A_y) を勝手に 0 とおく（＝Aをローラー支持とみなす）と， [ S_1+S_2=P,\quad S_1 a+S_2 b=Pl ] から ① が出ます。しかし本問のAはピン支持で (A_y\neq0) も取り得るため不適切。 実際，①は (a=b) で発散し，物理的に不合理です。

まとめ：この手の「剛体棒＋複数のバネ（鋼線）」は静力学＋適合条件が必須です。