答え：① (\displaystyle \omega=\sqrt{\frac{k}{m}}\cos\alpha)（厳密には (|\cos\alpha|)。）
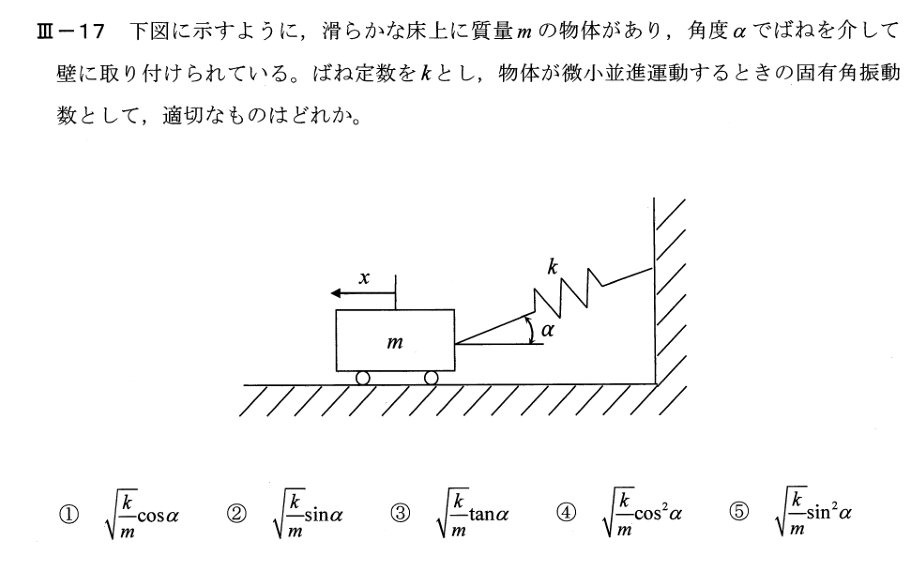
考え方（水平微小振動）
- ばね定数：(k)（ばね軸方向のフックの法則）
- ばねは水平方向に対して角度 (\alpha)
- 小さな水平変位を (x) とする（左向きを正）
1) ばねの伸び
質点が水平に (x) だけ動くと、ばね軸方向の伸びは [ \Delta \ell = x\cos\alpha ] （変位ベクトルのばね方向成分）2) ばね力の水平成分
ばね力の大きさ：(k,\Delta \ell = k,x\cos\alpha)（ばね軸向き） その水平成分はさらに (\cos\alpha) を掛けて [ F_x = k,x\cos\alpha\cdot \cos\alpha = k,\cos^2\alpha ; x ] 向きは変位と逆（復元力）。3) 運動方程式 → 固有角振動数
[ m\ddot x + k\cos^2\alpha ; x = 0 \quad\Rightarrow\quad \omega=\sqrt{\frac{k\cos^2\alpha}{m}} =\sqrt{\frac{k}{m}};|\cos\alpha| ] 通常は (\alpha\in[0,\pi/2]) を想定するので (\cos\alpha\ge0)、選択肢では ①。チェック
- (\alpha=0^\circ)（水平ばね）→ (\omega=\sqrt{k/m})（一致）
- (\alpha=90^\circ)（鉛直ばね）→ (\omega=0)（水平復元力なし）
その水平成分はさらに \cos\alpha を掛けてを詳しく教えて下さい
もちろん詳しく説明します。 ここが一番つまずきやすいポイントなので、ベクトルの向きと成分分解に絞って丁寧に解説します。✅ 問題の状況整理
ばねは 壁と質点を結ぶ方向にあり、その方向は水平と角度 (\alpha) をなしています。 質量 (m) を左向きに微小量 (x) 動かすと、ばねの 伸び（ばね軸方向の変位） は [ \Delta \ell = x\cos\alpha ] になります。✅ 1. ばねは「ばね軸方向」にしか力を出さない
ばね力の大きさは [ F_{\text{spring}} = k,\Delta\ell = k x \cos\alpha ] これは「ばねの向き（斜め方向）」の力の大きさであって、まだ水平成分ではありません。✅ 2. その力を「水平・鉛直」に成分分解する必要がある
下図を頭に浮かべてください： ／（ばね方向：角度α ）
F_s ／|
/ |
----→ 水平方向（欲しい成分）
✅ ❗ここが重要（よく誤解される点）
- 最初の (\cos\alpha) は 「水平変位 (x) がばね軸方向にどれだけ伸びを作るか」
- 2番目の (\cos\alpha) は 「ばね軸方向の力を水平成分に射影する係数」
✅ 図で説明（文章図解）
質点が左へ (x) 動く ← x
斜め方向への投影 = x cos α
斜め方向へ k (x cos α)
水平成分 = k (x cos α) × cos α
✅ だから最終的に
[ F_x = k x \cos^2\alpha ] この水平復元力が運動方程式に入るため [ m\ddot x + k\cos^2\alpha , x = 0 ] 固有角振動数は [ \omega = \sqrt{\frac{k\cos^2\alpha}{m}} = \sqrt{\frac{k}{m}} \cos\alpha ]✅ まとめ（超重要点）
| 出てくる (\cos\alpha) | 意味 |
|---|---|
| ① 変位の投影 | 水平方向 (x) → ばね方向の伸び |
| ② 力の投影 | ばね力 → 水平方向の成分 |
必要なら、 ✅ 図をより細かく分解した説明 ✅ エネルギー法で導く方法（等価ばね定数を出す別解） も説明できます！
