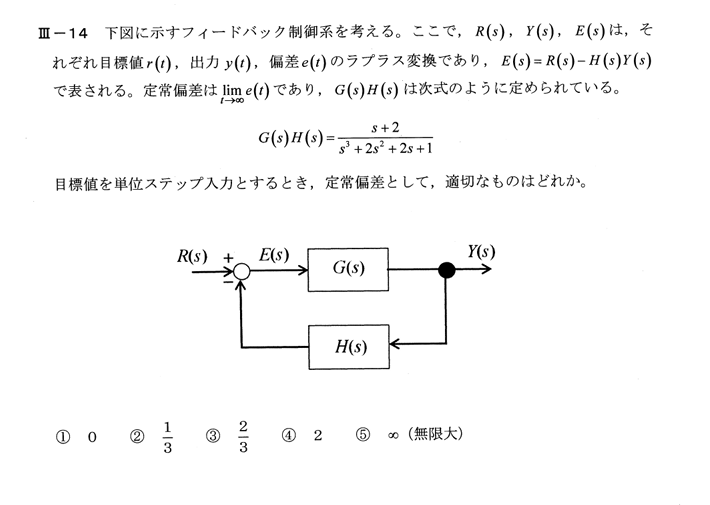
$E(s)=R(s)-H(s)Y(s)=R(s)-H(s)E(s)G(s)$

式を変形して、$R(s)=\frac{1}{s}$を代入すると

$⇔E(s)=\frac{R(s)}{G(s)H(s)+1}=\frac{\frac{1}{s}}{\frac{s+2}{s^3+2s^2+2s+1}+１}$

最終値の定理を用いて、

$\displaystyle \lim_{ t \to \infty }e(t)=\displaystyle \lim_{ s \to 0 }s・E(s)=\displaystyle \lim_{ s \to 0 }s・\frac{\frac{1}{s}}{\frac{s+2}{s^3+2s^2+2s+1}+１}＝1/3$

[解答]②

参考

誤差伝達はどのように導出しましたか？

 

誤差伝達
[
\frac{E(s)}{R(s)}=\frac{1}{1+G(s)H(s)}
]
がどこから出てくるかを、ブロック線図の式づくりから丁寧に導出します。

---

✅ 1. ブロック線図の関係式を書く

ブロック線図を見ると、

      +───→ E(s) ──→ G(s) ──→ Y(s)
      ↑                 │
      │                 ↓
     R(s) <──────── H(s)──

負帰還なので誤差信号は

[
\boxed{E(s)=R(s)-H(s)Y(s)}
]

出力は

[
\boxed{Y(s)=G(s)E(s)}
]

この2式だけで系のふるまいが決まります。

---

✅ 2. E(s) を R(s) だけの式にしたい

上の2式を連立します。

まず
[
Y(s)=G(s)E(s)
]
を
[
E(s)=R(s)-H(s)Y(s)
]
に代入する。

---

✅ 3. 代入して整理

[
E(s) = R(s)-H(s),Y(s)
= R(s)-H(s),G(s),E(s)
]

両辺を E(s) についてまとめる：

[
E(s)+H(s)G(s)E(s)=R(s)
]

[
E(s){1+G(s)H(s)}=R(s)
]

---

✅ 4. 誤差伝達関数の完成

[
\frac{E(s)}{R(s)}=\frac{1}{1+G(s)H(s)}
]

これで、誤差伝達関数が完成します。

---

✅ 5. まとめ（本質）

負帰還では

• 誤差 (E) が入力となってG(s)へ入る
• 出力 (Y) が H(s) を通って戻ってくる
• 誤差は “入力 − 戻り”

という構造になっているため、必ず

[
E = \frac{R}{1+GH}
]

が生まれます。

---

✅ 6. 簡易図で理解するとこう

入力 R
 ↓
[ 1 / (1 + G H ) ] ←── 誤差 E

負帰還を入れると、入力が 1 / (1 + GH) だけ小さくなって誤差となる。

---

必要なら
✅ 同じ方法で出力伝達関数 (Y/R = G/(1+GH)) の導出
✅ ループゲイン GH の意味
✅ タイプ0/1/2系の定常偏差の一覧
も説明できます！

 

最終値の定理とはなんですか？

 

最終値の定理（Final Value Theorem）は、
時間領域での定常値（t→∞ の値）を、ラプラス領域から直接求められる便利な定理です。

結論から書くと…

---

✅ 最終値の定理（Final Value Theorem）

ラプラス変換された関数 (F(s)) があるとき、時間領域での最終値は

[
\boxed{
\lim_{t\to\infty}f(t)=\lim_{s\to 0} sF(s)
}
]

ただし条件が必要（後述）。

---

✅ 1. なぜこんな定理が便利なのか？

制御工学では「定常偏差」など、

• (e(t)) が (t\to \infty) でどうなるか？
• 出力 (y(t)) が定常状態では何になるか？

を知りたいことが多い。

しかし、いちいち逆ラプラス変換して (t\to∞) を調べるのは大変。

そこで
[
sE(s)\ \text{の}\ s\to 0
]
だけ見ればよい、という魔法の定理が“最終値の定理”。

---

✅ 2. 使い方の例（今回の問題）

今回の問題では

[
e_\infty=\lim_{t\to\infty}e(t)
=\lim_{s\to0} sE(s)
]

ステップ入力 (R(s)=1/s) の場合

[
sE(s)=\frac{s}{1+G(s)H(s)}\cdot\frac{1}{s}
=\frac{1}{1+G(s)H(s)}
]

よって

[
e_\infty=\frac{1}{1+G(0)H(0)}
]

というように、逆ラプラス変換なしで答えが出る！

---

✅ 3. どんなときに使える？（重要）

最終値の定理が成立するための条件：

✅ 系が安定

つまり、
伝達関数の極（閉ループの極）が右半平面にないこと。

特に

• 原点より右側に極があれば、発散するので定常値が存在しない。
• 虚軸上に極がある（例：s = 0 の2重極）と成立しない。

✅ f(t) の最終値が有限に存在すること

（発散する信号に最終値の定理は使えない）

---

✅ 4. 直感的な意味（理解しやすくする）

ラプラス変換
[
F(s) = \int_0^\infty f(t)e^{-st}dt
]

ここで (s \to 0) にすると
[
e^{-st} \to 1
]

つまり、
「関数全体の積分」に近づく。

さらに
[
sF(s)
]
を考えると、時間が長くなる部分が強調されて

“最終的な値” を取り出す効果になる。

---

✅ 5. 図で直感をつかむ（文章図解）

f(t)
│        ────→（定常値）
│      /
│    /
│  /
└─────────────→ t

ラプラス領域で s を 0 に寄せていくと、
時間が長い部分の情報が浮き上がり、
定常値が抽出される。

---

✅ 6. 最終値の定理と対になる「初期値の定理」

[
f(0^+)=\lim_{s\to\infty} sF(s)
]

“初期値”は「高周波成分（s→∞）」を見る。

最終値は「低周波成分（s→0）」を見る。

と対応している。

---

✅ まとめ

名称	内容
最終値の定理	(\lim_{t\to∞}f(t)=\lim_{s\to0}sF(s))
有効条件	閉ループが安定、虚軸上に極がない
便利な場面	定常偏差・定常出力の計算
直感	(s→0) は“低周波→長時間”を意味する

---

必要なら、
✅ なぜ s→0 が“長時間”を意味するのか
✅ 最終値の定理が使えない反例
✅ 初期値との比較
もさらに詳しく説明できます！

初期値との比較をお願いします

 

了解！
ここでは 初期値の定理 vs 最終値の定理 を、
意味 → 数式 → 図解 → 直感的イメージ
の順で比較しながら解説します。

---

✅ 1. まず結論（2つの定理）

● 初期値の定理（Initial Value Theorem）

[
\boxed{f(0^+)=\lim_{s\to\infty}sF(s)}
]

● 最終値の定理（Final Value Theorem）

[
\boxed{\lim_{t\to\infty} f(t)=\lim_{s\to 0} sF(s)}
]

初期値 ⇒ s→∞
最終値 ⇒ s→0

ここが最大のポイント。

---

✅ 2. なぜ s→∞ で初期値が取れるのか？

ラプラス変換は
[
F(s)=\int_0^\infty f(t)e^{-st}dt
]

s→∞ のとき e^{-st} が超急速減衰 するので、
t=0 付近しか“見えない”。

例：
[
e^{-1000t} \Rightarrow t>0.01s でほぼゼロ
]

したがって
s→∞ にすると「時間の初めの様子」だけ抽出される。

例（一次遅れ）
[
f(t)=1-e^{-t},\quad F(s)=\frac{1}{s}-\frac{1}{s+1}
]

初期値は
[
\lim_{s\to\infty}sF(s)=1-1=0=f(0)
]

---

✅ 3. なぜ s→0 で最終値が取れるのか？

s→0 では
[
e^{-st}\to1
]

つまり時間方向に対して
長時間の影響が強くなる。

簡単に言うと：

• 初期値は“高周波成分（s大）”に支配される
• 最終値は“低周波成分（s小）”に支配される

だから
[
sF(s)\text{の }s\to0
\Rightarrow\text{定常状態の値を抽出}
]

---

✅ 4. 直感イメージ（図解）

● 初期値の定理

f(t)
↑│\
 │ \
 │  \   ← 初期の形だけ重要
 │   \
───┴──────── t
     0  1

sを大きくすると、t=0付近に
ズームインするような効果がある

● 最終値の定理

f(t)
│        ────→  (定常値)
│      /
│    /
│  /
└────────────── t

sを小さくすると、t→∞ の部分が
強調される（低周波成分）

---

✅ 5. 正確な使用条件（重要）

定理	使える条件
初期値の定理	f(t) が T=0 で有界。インパルス成分があってもOK
最終値の定理	安定系であることが必須（右半平面 or 虚軸上に極がない）

特に最終値定理は
閉ループが不安定なら絶対に使えない
（振幅が発散し、t→∞ の値が存在しないため）

---

✅ 6. 数式での対応関係（美しい対称性）

項目	初期値の定理	最終値の定理
対応する極領域	s→∞	s→0
物理意味	高周波 → 初期挙動	低周波 → 定常挙動
抽出されるもの	f(0⁺)	f(∞)
どこで使う？	初期条件付きの問題	定常偏差の計算

---

✅ 7. 最後に超短まとめ

• s→∞（高周波）を見ると → 初期値がわかる
• s→0（低周波）を見ると → 最終値（定常値）がわかる
• 最終値は安定系でしか使えない
• 初期値はほぼすべての系で使える

---

必要なら、
✅ 初期値定理の証明
✅ 最終値定理の証明
✅ 両者が破綻する例（RHP極の例）
などもできます！

ラプラス変換のメリットはなんですか？

 

ラプラス変換の“すごさ”は、
時間領域の面倒くさい微分方程式を、代数（足し算・掛け算）に変えてしまう
という点にあります。

数学を魔法に変えてしまう感じです。

ここでは、直観的メリット → 工学的メリット → 数学的メリット
の順に整理します。

---

✅ 1. まず直感から：

微分方程式が“ふつうの方程式”に変わる！

例えば

[
m\ddot{x}+c\dot{x}+kx = f(t)
]

これは時間領域では

• 微分がある
• 時間変化がある
• 解析が面倒

でもラプラス変換すると

[
(m s^2 + c s + k)X(s) = F(s)
]

ただの代数式。
微分は
[
\frac{d}{dt} \rightarrow s
]
になる。

✅ だから 解くのが圧倒的に簡単になる。

---

✅ 2. 工学的メリット（制御・機械・電気で重要）

✅ (1) 微分方程式が代数方程式になる

→ ブロック線図、伝達関数、フィードバック解析が可能。

✅ (2) 初期条件を自動で含められる

[
L{\dot{x}} = sX(s)-x(0)
]

→ 初期値を勝手に入れてくれる。

✅ (3) 伝達関数 G(s) が扱える

振動・制御・電気回路のふるまいを
たった G(s) という関数ひとつで扱える。

✅ (4) 安定性が極（s平面）で一瞬で判断できる

• 右半平面に極がある → 不安定
• 左半平面 → 安定

直感でわかる！

✅ (5) 最終値の定理・初期値の定理が使える

→ 逆変換なしで結果が出る。

✅ (6) 畳み込み積分が単なる掛け算に

[
y(t)=f(t)*g(t)
\quad\Rightarrow\quad
Y(s)=F(s)G(s)
]

→ 応答計算が爆速で終わる。

---

✅ 3. もっと深いメリット（周波数領域で考える）

✅ (1) s = σ + iω （複素数）なので

減衰＋振動を 1本の複素平面で同時に扱える

例：

• 振動成分 → (iω) 軸
• 減衰成分 → σ 軸

✅ (2) 周波数応答・Bode線図・共振周波数が自然に出てくる

[
G(i\omega)
]
を見れば

• 増幅度
• 位相遅れ
• 共振現象
  が全て分かる。

---

✅ 4. 例で見るとわかりやすい

例：ステップ応答を求めたい

時間領域なら
微分方程式を解く
→ 定数項合わせる
→ 初期条件入れる
→ 計算がしんどい

ラプラスなら

[
R(s)=\frac{1}{s}
]
[
Y(s)=G(s)R(s)
]
[
y(t)=\mathcal{L}^{-1}{Y(s)}
]

伝達関数の掛け算だけで終わり。

---

✅ 5. ざっくりまとめ（本質だけ）

メリット	理由
微分が s に置き換わる	微分方程式が代数方程式になる
初期条件が自動で入る	(sX(s)-x(0)) の項
畳み込みが掛け算に	応答解析が簡単
周波数特性がわかる	(G(i\omega)) がそのまま周波数応答
安定性がわかる	s 平面の極の位置
制御工学に必須	伝達関数で一瞬でモデル化

---

✅ 超直感イメージ

ラプラス変換は

「時間の世界」→「周波数＋減衰の世界」への変換。
時間の複雑な絡み合いを、
一本の複素数 s 軸に全部押し込む“魔法の圧縮”みたいなもの。

---

必要なら、
✅ ラプラス変換とフーリエ変換の違い
✅ ラプラス変換の厳密な定義と収束領域
✅ なぜ微分が s になるのかの証明
なども解説できます！

 

目標値は入力値を入れるのに目標値というのはなぜですか？

 

ここは 制御工学の言葉のクセが原因で、最初は必ず混乱します。
実は “入力値” と “目標値（指令値）” は、同じ場合と違う場合があるんです。
順を追って、非常に明快に説明します。

---

✅ 結論（これが最も大事）

目標値（reference）とは、“システムにやらせたい動き・状態”。
それを数値として入力するので、
結果として R(s) が「入力」であり「目標値」になる。

つまり
[
\text{入力}＝\text{目標値}
]
ではなく、

[
\text{入力}の中でも特に「目標とする値」をR(s)と呼ぶ。
]

---

✅ 1. 普通の物理では “入力＝外から加えたもの”

例えば質点に力を加えるなら

• 力 → 入力
• 変位 → 出力

これは直感的。

---

✅ 2. しかし制御では「やらせたい動作」が最優先

制御の目的は
装置を思い通りの動きにさせること。

だから、
人間（または上位システム）が設定する「望む値」を
目標値（set point / reference） と呼びます。

例えば：

• ロボットのアーム角度を 30° にしたい
  → 30° が目標値
• モーターを毎分 1500 rpm にしたい
  → 1500 rpm が目標値
• 温度を 70℃ にしたい
  → 70℃ が目標値

そしてシステムへ「30°」を数値として入力する。この入力信号を
[
R(s)
]
と書く。

---

✅ 3. “入力＝目標値” と言われる理由

入力という言葉は広すぎる

だから制御ではもっと意味の特定された言葉が必要。

用語	意味
入力（input）	システムに与えるすべての信号
目標値（reference）	望む動作・状態の値
外乱（disturbance）	望まない入力（風、摩擦、衝撃など）

つまり「入力の中の一部」である
“目標として与える信号” だけを特別に R と呼ぶ。

そのため、
R(s) は「入力信号」なのに “目標値” と呼ばれる。

---

✅ 4. ブロック線図でみると一目瞭然

   目標値 R(s)  → (+) → E(s) → G(s) → Y(s)
                     ↑
                     └── H(s) ────

ここで

• R(s)：やりたいこと（目標）
• Y(s)：実際の出力
• H(s)：フィードバック
• E(s): 誤差 = R − H·Y

✅ 目標値は “入力” ではなく “基準値”

“これに近づけるために制御する値” だから。

---

✅ 5. なぜ「入力値」と言わず「目標値」と言うのか

理由は 3 つあります：

✅① 入力には「外乱」も含まれる

目標値ではない。

✅② 制御対象に強制力を加える「操作量（入力）」とも区別したい

たとえばモーターなら

• 目標値 → 回転数の希望値
• 入力 → モータへの電圧（制御系が決める）
  これはまったく別物。

✅③ 目標値は人間がシステムに与える“指令”だから

操作入力とは役割が違う。

---

✅ 6. 名称の対応を整理しておくと理解が速い

名前	主な役割
目標値 R(s)	やらせたい状態・位置・速度
誤差信号 E(s)	R − H·Y （制御の原動力）
操作量 U(s)	アクチュエータへ送る信号（制御器の出力）
出力 Y(s)	実際の応答
外乱 D(s)	望まない入力

---

✅ まとめ

目標値とは、
「制御で実現したい値（指令値）を “入力信号として” 入れるもの」。

だから

• 入力信号ではある
• しかし単なる入力ではなく「目標」なので R(s) と特別に呼ぶ

というだけです。

---

必要なら：

✅ ブロック線図での R(s), U(s), Y(s), D(s) の役割
✅ 制御系の「入力」「目標」「外乱」「操作量」の違い
✅ PID 制御における目標値の具体例

なども詳しく説明できます！