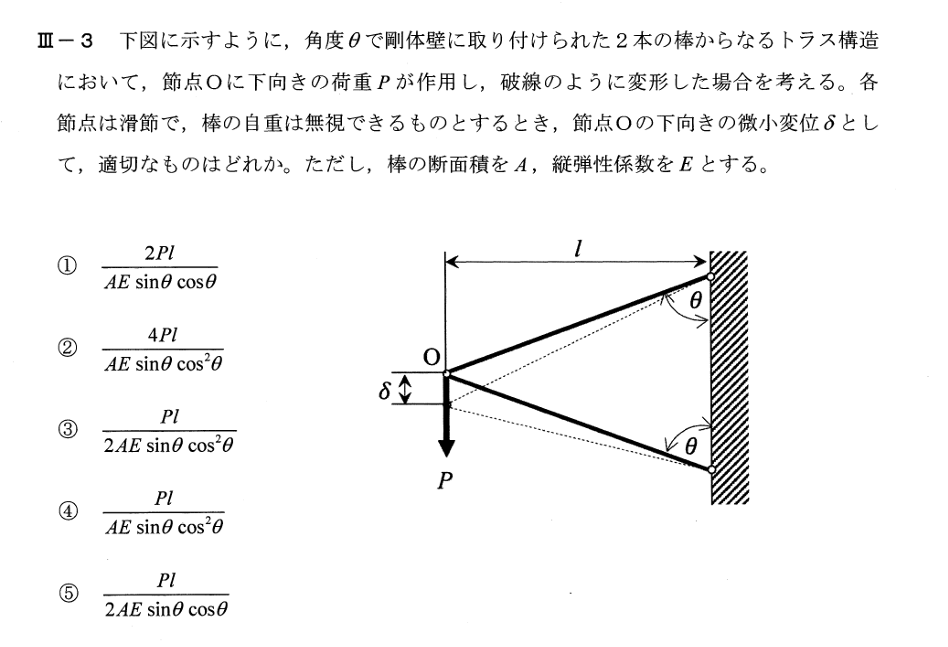
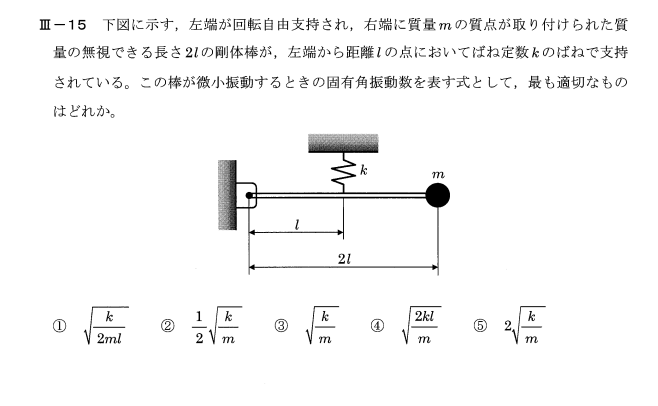
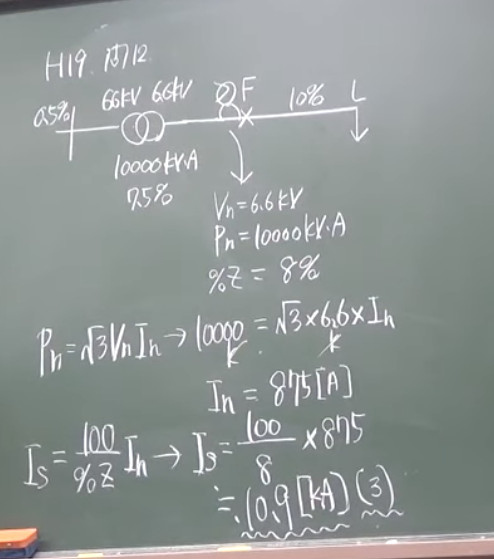均質な断面をもつ Euler–Bernoulli 梁の自由曲げ振動の運動方程式は，単位長さ当たり質量 $ρA$ による慣性項と，曲げ剛性 $B$ による４次微分項のバランスで表されます。すなわち $$ρA\,\frac{\partial^2 w}{\partial t^2} + B\,\frac{\partial^4 w}{\partial x^4}=0$$   となるので，選択肢①が正解です。   参考：技術士第一次試験－令和2年度機械部門Ⅲ-22解答例 | 技術士のたまご

導出過程の解説してください

以下の手順で，均質な Euler–Bernoulli 梁の自由曲げ振動方程式 $$ρA\,\frac{\partial^2 w}{\partial t^2} + B\,\frac{\partial^4 w}{\partial x^4} = 0$$   を導出します。

---

1. モデル化と仮定

1. 梁は長さ方向 $x$  に沿って細長く，断面は均質で変化しない。
2. 変形は小振幅で，断面が変形せず「断面は変形前と平行に保たれる」（Plane sections remain plane）．
3. 軸方向変形やせん断ひずみは無視し，曲げのみを扱う（Euler–Bernoulli 仮定）。

---

2. 曲げモーメント–曲率関係

材料のヤング率 $E$ ，断面２次モーメント $I$ を用いると，曲げ剛性 $B=EI$ に対して， $$M(x,t) = B\,\frac{\partial^2 w(x,t)}{\partial x^2}$$   が成り立ちます。ここで $w(x,t)$ は梁のたわみです。

---

3. せん断力の定義

曲げモーメントが $x$ 方向に変化すると，せん断力 $Q(x,t)$ が生じ， $$Q(x,t) = \frac{\partial M}{\partial x} = B\,\frac{\partial^3 w}{\partial x^3}.$$  

---

4. 微小要素 $dx$

 

の垂直力釣り合い

梁の微小要素 $[x,\,x+dx]$ を取り，垂直方向力の釣り合いを考えると， 左端で受ける $Q(x)$ と右端で受ける $Q(x+dx)$ の差が，その要素の慣性力になる： $$Q(x) - Q(x+dx) \;=\; ρA\,dx\;\frac{\partial^2 w}{\partial t^2}.$$   両辺を $dx$ で割り， $dx\to0$ とすると， $$-\,\frac{\partial Q}{\partial x} = ρA\,\frac{\partial^2 w}{\partial t^2}.$$  

---

5. せん断力 $Q$

 

の展開

上記の $Q=B\,\partial^3w/\partial x^3$ を代入すると， $$-\,B\,\frac{\partial}{\partial x}\Bigl(\frac{\partial^3 w}{\partial x^3}\Bigr) = ρA\,\frac{\partial^2 w}{\partial t^2} \quad\Longrightarrow\quad -\,B\,\frac{\partial^4 w}{\partial x^4} = ρA\,\frac{\partial^2 w}{\partial t^2}.$$  

---

6. 最終形

両辺に $-1$ を掛けて整理すると，最終的に $$\boxed{$$   が得られます。 以上が，Euler–Bernoulli 梁の自由曲げ振動方程式の導出過程です。