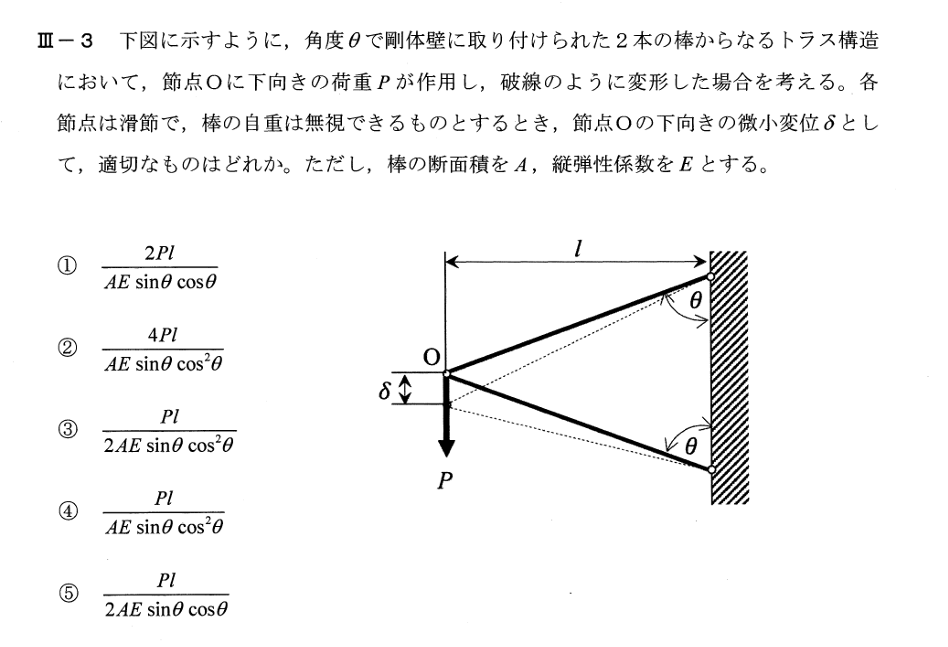
水平方向と鉛直方向に対して力のつりあいを考えると，
$P_{\rm OA}sinθ + P_{\rm OB}sinθ = 0$
$P_{\rm OA}cosθ - P_{\rm OB}cosθ -P = 0$
より、
$P_{\rm OA} ＝ -P_{\rm OB} = \frac{P}{2cosθ}$
よって部材OA，部材OBの伸びはそれぞれ
$\lambda_{\rm OA} = \varepsilon_{\rm OA} \frac{l}{sinθ} = \frac{P_{\rm OA} l}{E Asinθ} = \frac{Pl}{2E Acosθsinθ}$
$\lambda_{\rm OB} = \varepsilon_{\rm OB} \frac{l}{sinθ} = \frac{P_{\rm OB} l}{E Asinθ} = -\frac{Pl}{2E Acosθsinθ}$
微小変化した範囲の三角に着目して、λ ＝ δ cos θ.
$\frac{Pl}{2E Acosθsinθ} = δ cos θ$
⇔$ δ ＝\frac{Pl}{2AEsinθcos^2θ}$
[解答]③
参考
第4回 トラス
さらに詳しく解説して下さい
答えは ③ (\displaystyle \delta=\dfrac{P,l}{2AE,\sin\theta,\cos^2\theta}) です。 （(\theta) は 棒と鉛直のなす角。図の表記どおり、壁の法線＝鉛直に対して角度 (\theta) です。）じっくり導出（力のつり合い＋幾何拘束）
1) 幾何
- 壁から節点 O までの水平距離が (l)。
- 各棒の実長は [ L=\frac{l}{\sin\theta} ] （水平成分が (L\sin\theta) で、それが (l)）
2) 力のつり合い → 棒軸力 (T)
節点 O に鉛直下向き荷重 (P)。左右対称なので上下 2 本の棒に同じ軸力 (T) が生じる。 棒の鉛直成分は各々 (T\cos\theta)（棒と鉛直のなす角が (\theta) なので）。 鉛直つり合い： [ 2,T\cos\theta = P \quad\Rightarrow\quad \boxed{T=\dfrac{P}{2\cos\theta}} ]3) 伸びと節点変位の関係（幾何学）
各棒の軸方向伸び： [ \Delta = \frac{T,L}{AE} ] 節点 O が鉛直に (\delta) だけ下がると，その鉛直変位の棒方向成分は [ \delta\cos\theta ] （“鉛直方向”と“棒方向”のなす角が (\theta) だから、射影係数は (\cos\theta)） 小変位の範囲では，この射影がそのまま棒の伸びに等しい： [ \Delta = \delta\cos\theta ]4) まとめて解く
[ \delta\cos\theta=\frac{T,L}{AE} =\frac{1}{AE},\frac{P}{2\cos\theta},\frac{l}{\sin\theta} ] [ \Rightarrow\quad \boxed{\delta=\frac{P,l}{2AE,\sin\theta,\cos^{2}\theta}} ]別解（等価鉛直剛性で見る）
棒 1 本の軸方向剛性は (k_a=AE/L)。 その鉛直方向成分剛性は [ k_v = k_a \cos^2\theta=\frac{AE}{L}\cos^2\theta ] （方向余弦の二乗則）。2 本並列なので合成剛性 [ K = 2,\frac{AE}{L}\cos^2\theta ] したがって [ \delta=\frac{P}{K} =\frac{P,L}{2AE\cos^2\theta} =\frac{P}{2AE\cos^2\theta}\cdot\frac{l}{\sin\theta} =\frac{P,l}{2AE,\sin\theta,\cos^{2}\theta}. ]妥当性チェック
- (\theta\to 90^\circ)（棒が水平）：(\cos\theta\to0\Rightarrow \delta\to\infty)。 鉛直荷重を支える成分がなくなり、剛性 0 → 合理的。
- (\theta\to 0^\circ)（棒が鉛直）：(\sin\theta\to0) で (\delta\to0)。 ほぼ鉛直棒 2 本で非常に硬い → 合理的。
δ＝Δcosθではないですか？ δだけさがると、伸びΔのcos成分になりませんか？
いい質問です。結論だけ先に──結論
この図の角度 (\theta) は棒と“鉛直”のなす角です。 節点 (O) が鉛直下向きに (\delta) だけ動くとき，各棒の軸方向伸び (\Delta) は [ \boxed{;\Delta=\delta\cos\theta;} \qquad\Leftrightarrow\qquad \boxed{;\delta=\dfrac{\Delta}{\cos\theta};} ] です。 したがって (\delta=\Delta\cos\theta) ではありません（逆です）。なぜそうなるか（ベクトルの投影で一発）
- 節点の変位ベクトル：(\mathbf{d}=(0,-\delta))（鉛直下向き）
- 棒の単位ベクトル（軸方向）：(\mathbf{u}=(\sin\theta,\pm\cos\theta)) （鉛直となす角が (\theta) なので縦成分が (\cos\theta)）
これを使って先の答えが出るかチェック
各棒の軸力はつり合いより [ 2N\cos\theta=P ;\Rightarrow; N=\frac{P}{2\cos\theta}. ] 棒の長さは (L=\dfrac{l}{\sin\theta})（水平距離が (l)）。 軸方向伸びは (\displaystyle \Delta=\frac{N L}{AE} =\frac{P}{2\cos\theta}\cdot\frac{l}{AE\sin\theta} =\frac{Pl}{2AE\sin\theta\cos\theta}). 上の幾何関係 (\delta=\Delta/\cos\theta) を使うと [ \boxed{\delta=\frac{Pl}{2AE,\sin\theta,\cos^2\theta}}, ] となり、選択肢③（(\displaystyle \frac{Pl}{2AE\sin\theta\cos^2\theta})）と一致します。直感メモ
- 棒と鉛直の角が (\theta) なので、鉛直変位の“棒方向成分”は (\cos\theta)。
- だから「節点の鉛直変位 (\delta) → 棒の伸び (\Delta)」は (\Delta=\delta\cos\theta)（掛ける）であり、 逆に「棒の伸びから節点の鉛直変位」を求めるときは割る：(\delta=\Delta/\cos\theta)。
引っ張りにより発生する応力による伸びと移動による伸びは同じですか
ここ、とても大事なポイントです。 「力による伸び（材料の変形）」と「節点の移動によって生じる見かけの伸び（幾何学的伸び）」は、一般には別物です。 しかし トラス構造の解析では“微小変形”を仮定するため、２つが一致するように扱います。✅ 結論（微小変形の範囲では）
[ \boxed{\text{軸方向力から計算した伸び } \Delta_{\text{力}} ;=; \text{節点変位の投影から得られる伸び } \Delta_{\text{幾何}} } ] になります。 だからトラス構造では 「引張力から AE で割って求めた伸び」と 「節点が動いたことによる棒の伸び」 を同じ (\Delta) として使います。✅ 1. 力による伸び（材料力学）
軸方向の引張力 (N) による伸びは [ \Delta_{\text{力}}=\frac{N L}{A E} ] で、 材料の弾性変形（フックの法則）から求めるものです。✅ 2. 節点の移動による“幾何学的伸び”
節点が動くと、棒が少し傾いたり位置が変わって 見かけ上、棒の長さが変わります。 今回の場合は棒と鉛直の角 (\theta) なので、節点が (\delta) 下がると： [ \Delta_{\text{幾何}}=\delta \cos\theta ] （変位の棒方向成分をとっただけ）✅ 3. トラスの仮定（超重要）
トラス構造では以下を仮定します：✅ 微小変形
変形が非常に小さいので- 角度の変化
- 長さの変化
- 位置の変化
✅ 4. もし変形が大きいとどうなるか？
実は一致しません。- 節点が大変位すると方向余弦が変わる
- 伸びを引起す形状変化と、応力による伸びが非線形になる
✅ 5. 今回の問題での使い方
棒の伸び (\Delta) は- 力のつり合いで軸力 (N) を求めて (\Delta = \frac{NL}{AE})
- 幾何学から (\Delta = \delta\cos\theta)
✅ まとめ（今回の質問に直接回答）
◆ Q：引っ張りによる伸びと、節点が動いたことによる伸びは同じですか？
→ 微小変形を仮定するトラスでは“同じ”として扱われます。 ただし、- 材料力による伸び
- 配置の変化による伸び
もっと図を描きながら解説することもできますし、 この「微小変形の仮定」がどこまで安全なのかも説明できます。
