令和5年度技術士第一次試験問題［基礎科目］　問Ⅰ-2-2　ユークリッドの互除法

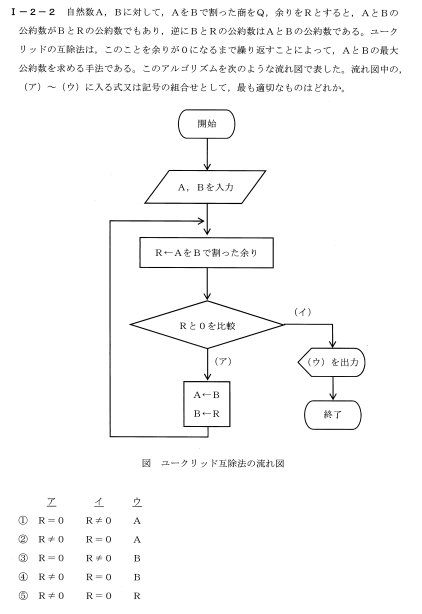
  ### ユークリッドの互除法の手順 ユークリッドの互除法は、次の手順で最大公約数を求めます。 1. 2つの数 \( A \) と \( B \) が与えられたとき、\( A \) を \( B \) で割った余り \( R \) を求めます。 2. もし余り \( R = 0 \) なら、\( B \) が最大公約数です。 3. 余りが 0 でない場合、\( A \) を \( B \) に、\( B \) を \( R \) に置き換え、再度手順1から繰り返します。 [解答]④ 参考： 過去問ドットコム  

自然数A，Bに対して、AをBで割った商をQ、余りをRとすると、AとBの公約数がBとRの公約数でもあり、逆にBとRの公約数はAとBの公約数である というのを具体的に教えてください

この内容は、ユークリッドの互除法の基礎となる性質であり、2つの数 \( A \) と \( B \) の最大公約数を求めるために利用される数学的な性質です。この性質を具体例を使って説明します。 ### 前提条件 自然数 \( A \) を \( B \) で割ったときの商を \( Q \)、余りを \( R \) とすると、次のように表せます。 \[ A = B \times Q + R \] このとき、以下の性質が成り立ちます： 1. \( A \) と \( B \) の公約数は \( B \) と \( R \) の公約数でもある。 2. \( B \) と \( R \) の公約数は \( A \) と \( B \) の公約数でもある。 この性質を用いることで、最大公約数を段階的に簡略化して求めることができます。 ### 具体例 例として、\( A = 48 \) と \( B = 18 \) の場合を考えます。 1. **最初の割り算** \[ A = 48, \quad B = 18 \] \( A \) を \( B \) で割ったとき、商 \( Q = 2 \) で余り \( R = 12 \) です。 \[ 48 = 18 \times 2 + 12 \] このとき、48と18の公約数は、18と12の公約数でもあることが言えます。 2. **次の割り算** 今度は、18を12で割ります。 \[ A = 18, \quad B = 12 \] 商 \( Q = 1 \) で余り \( R = 6 \) です。 \[ 18 = 12 \times 1 + 6 \] このとき、18と12の公約数は、12と6の公約数でもあることが言えます。 3. **さらに次の割り算** 次に、12を6で割ります。 \[ A = 12, \quad B = 6 \] 商 \( Q = 2 \) で余り \( R = 0 \) です。 \[ 12 = 6 \times 2 + 0 \] ここで余りが0になったため、\( B = 6 \) が48と18の最大公約数であることがわかります。 ### 結論 このように、\( A = B \times Q + R \) の形で割り算を繰り返していくと、最終的に余りが0になったときの割られる数が、最初の \( A \) と \( B \) の最大公約数となります。  

余りが公約数に関係してくるのですね

はい、その通りです！余りが公約数に関係しているというのが、ユークリッドの互除法の核心部分です。 具体的には、自然数 \( A \) と \( B \) の公約数は、\( A \) を \( B \) で割った余り \( R \) を使っても同じ公約数を持つ、という性質を利用しています。つまり、\( A \) と \( B \) の公約数は、次に取り扱う \( B \) と \( R \) の公約数と一致するのです。 ### なぜ余りが関係してくるのか 数式で表すと、次のように考えられます： \[ A = B \times Q + R \] このとき、もし \( D \) が \( A \) と \( B \) の公約数であるならば、\( D \) は \( B \) と \( R \) の公約数でもあります。逆に、もし \( D \) が \( B \) と \( R \) の公約数であれば、それは \( A \) と \( B \) の公約数にもなります。 この性質によって、最大公約数の問題を「余り \( R \) 」を使ってどんどん小さい数に変えていくことができ、最終的に割り切れるところ（余りが 0 になるところ）で最大公約数が得られるのです。 ### 実際の流れ ユークリッドの互除法では、次のような流れになります： 1. 2つの数 \( A \) と \( B \) から、余り \( R \) を求める。 2. 次に \( B \) と \( R \) で同じことを繰り返す。 3. これを余りが 0 になるまで続けると、最終的に最大公約数が求まる。 ### この方法のメリット ユークリッドの互除法によって、元々の数が非常に大きくても、効率よく最大公約数を求めることができます。このようにして、余りを使って段階的に問題を小さくしていくため、計算がシンプルで早くなるのです。 余りを使うことで、最大公約数を簡潔に求めることができるというのは、数学的に非常に優れた性質ですね！

Aが52、Bが27の場合はどうなりますか？

では、具体的に \( A = 52 \) と \( B = 27 \) の場合でユークリッドの互除法を使って最大公約数を求めてみましょう。 ### 手順 1. **最初の割り算** \[ A = 52, \quad B = 27 \] \( A \) を \( B \) で割ると、商 \( Q = 1 \) で余り \( R = 25 \) になります。 \[ 52 = 27 \times 1 + 25 \] 2. **次の割り算** 次に、\( B = 27 \) と \( R = 25 \) で同じことを行います。 \[ A = 27, \quad B = 25 \] 商 \( Q = 1 \) で余り \( R = 2 \) になります。 \[ 27 = 25 \times 1 + 2 \] 3. **さらに次の割り算** 次に、\( B = 25 \) と \( R = 2 \) で割り算を行います。 \[ A = 25, \quad B = 2 \] 商 \( Q = 12 \) で余り \( R = 1 \) になります。 \[ 25 = 2 \times 12 + 1 \] 4. **最後の割り算** 最後に、\( B = 2 \) と \( R = 1 \) で割り算を行います。 \[ A = 2, \quad B = 1 \] 商 \( Q = 2 \) で余り \( R = 0 \) になります。 \[ 2 = 1 \times 2 + 0 \] ここで余りが 0 になったため、最大公約数は \( B = 1 \) です。 ### 結果 \( A = 52 \) と \( B = 27 \) の最大公約数は **1** です。

=48 と=18の場合についてそれぞれの公約数をだしながら解説をすすめてください

では、\( A = 48 \) と \( B = 18 \) の場合について、ユークリッドの互除法を使いながら、それぞれの段階で公約数も確認していきましょう。 ### ステップ1: 初期の公約数 まず、48と18の公約数を見てみます。 - **48の公約数**: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48 - **18の公約数**: 1, 2, 3, 6, 9, 18 - **共通の公約数**: 1, 2, 3, 6 したがって、**48と18の公約数**は「1, 2, 3, 6」で、最大公約数は6です。ここでは確認のために一覧にしましたが、実際の計算ではユークリッドの互除法を使って効率よく最大公約数を求めます。 ### ユークリッドの互除法による計算 ユークリッドの互除法を使って、同じ最大公約数6が得られるか確認します。 #### 1. 最初の割り算 \[ A = 48, \quad B = 18 \] 48を18で割ると、商は2で余りは12です。 \[ 48 = 18 \times 2 + 12 \] この時点で、48と18の最大公約数は、18と12の最大公約数と同じになります。 #### 2. 次の割り算 次に、18を12で割ります。 \[ A = 18, \quad B = 12 \] 18を12で割ると、商は1で余りは6です。 \[ 18 = 12 \times 1 + 6 \] この時点で、18と12の最大公約数は、12と6の最大公約数と同じになります。 #### 3. 最後の割り算 次に、12を6で割ります。 \[ A = 12, \quad B = 6 \] 12を6で割ると、商は2で余りは0です。 \[ 12 = 6 \times 2 + 0 \] ここで余りが0になったため、**最大公約数は6**と分かります。 ### 結論 ユークリッドの互除法を使っても、48と18の最大公約数は6であることが確認できました。 ### まとめ このように、ユークリッドの互除法を使うと、初期の数からどんどん小さい数に変えていくことで、最大公約数を効率的に求めることができます。この方法は、数が非常に大きくても有効です。

計算の過程において最大公約数だけではなく、共通の公約数もかわらないですか？

ユークリッドの互除法の計算過程において、**最大公約数はもちろん、共通の公約数も変わりません**。これは、ユークリッドの互除法が次のような性質を持っているためです。 ### ユークリッドの互除法の性質 ユークリッドの互除法では、数 \( A \) と \( B \) の最大公約数を求める際に、\( A \) を \( B \) で割り、余り \( R \) を求めます。そして、次のステップでは \( A \) を \( B \)、\( B \) を \( R \) に置き換えて計算を続けます。この過程を繰り返すと、以下のような性質が成り立ちます。 1. \( A \) と \( B \) の共通の公約数は、\( B \) と \( R \) の共通の公約数でもある。 2. 逆に、\( B \) と \( R \) の共通の公約数は、元の \( A \) と \( B \) の共通の公約数でもある。 このため、割り算の過程で扱う2つの数（例えば、\( A \) と \( B \)、その後の \( B \) と \( R \)）は、**同じ共通の公約数を持ち続けます**。 ### 具体例での確認 もう一度、\( A = 48 \) と \( B = 18 \) の例で確認してみましょう。 1. 最初に、48と18の共通の公約数は「1, 2, 3, 6」です。 2. 48を18で割って、余りが12となったので、次に18と12の共通の公約数を考えます。18と12の共通の公約数も「1, 2, 3, 6」です。 3. さらに18を12で割って余りが6になるので、次に12と6の共通の公約数を考えます。12と6の共通の公約数も「1, 2, 3, 6」です。 4. 最後に12を6で割って余りが0になり、最大公約数が6であることがわかります。 ### 結論 このように、計算の過程において扱う数の組み合わせが変わっても、共通の公約数は変わりません。割り算を繰り返して数が変わっても、元の数の共通の公約数はそのまま維持されるというのがユークリッドの互除法の特徴です。