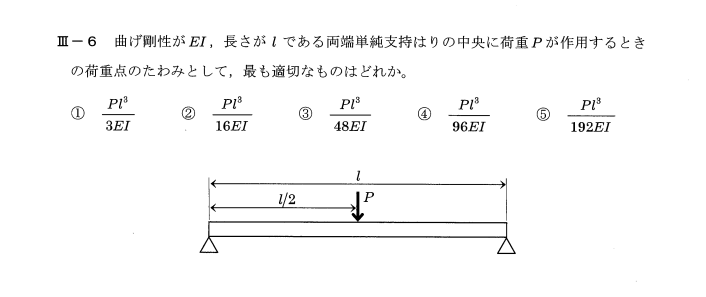
荷重Pがかかる梁のたわみは
$ \frac{ d^{2}y }{ dx^2 } = -\frac{ M(x) }{ EI }= -\frac{ Px }{ 2EI }$
となる。
上式を積分して、
$ \frac{ dy }{ dx } = -\frac{ Px^2 }{ 4EI } + C_1$
さらに積分して
$ ｙ = -\frac{ Px^3 }{ 12EI } + C_{1}x + C_2$
ここで梁の境界条件
ｘ＝0のとき、ｙ＝0
$ ｘ = \frac{ ｌ }{ 2 }$のとき、$θ = \frac{ dy }{ dx } = 0$
を代入すると、
$ C_1 = \frac{ Pｌ^2 }{ 16EI }、C_2 = 0$
となる。これらを代入すると
$ ｙ = -\frac{ Px^3 }{ 12EI } + \frac{ Pｌ^2 }{ 16EI }x$
従って、荷重点のたわみは
$ ｙ = -\frac{ Pl^3 }{ 96EI } + \frac{ Pｌ^3 }{ 32EI }＝\frac{ Pｌ^3 }{ 48EI }$
[解答] ③
両端単純支持のはりの場合、はりに荷重がかかっているとき単純支持点のたわみ角はどのようになりますか？
両端が壁に固定されたはりの場合、はりに荷重がかかっているとき単純支持点のたわみ角はどのようになりますか？
はりのたわみの理論に基づき、はりの支持条件や荷重の状態によって、たわみやたわみ角が異なる値を取ります。以下に、質問に関連する二つのシナリオについての簡単な説明を行います。
両端単純支持のはり:
この場合、はりの両端は垂直方向の変位を制約しますが、たわみ角（つまり、はりの端の角度変化）は0ではありません。そのため、たわみ角はゼロではなく、具体的な値は荷重の大きさや位置、はりの断面特性、材料特性によって決まります。
両端が壁に固定されたはり:
この場合、はりの両端は垂直方向の変位だけでなく、回転も制約します。そのため、たわみ角は0になります。中央部分では最大のたわみが発生しますが、両端でのたわみ角は0です。
たわみに必要な知識
◆たわみyとは、y方向のこと変形量のこと。
◆たわみ角θとは、たわんだ曲線の接線とx軸がなす角度のこと。
◆たわみの基礎式$ \frac{ d^{2}y }{ dx^2 } = ＋\frac{ M(x) }{ EI }$だけ覚える。
◆たわみの基礎式を1回積分したらたわみ角θが求まる。
◆たわみの基礎式を2回積分したらたわみｙが求まる。
参考：https://www.oribi.work/entry/Deflection
