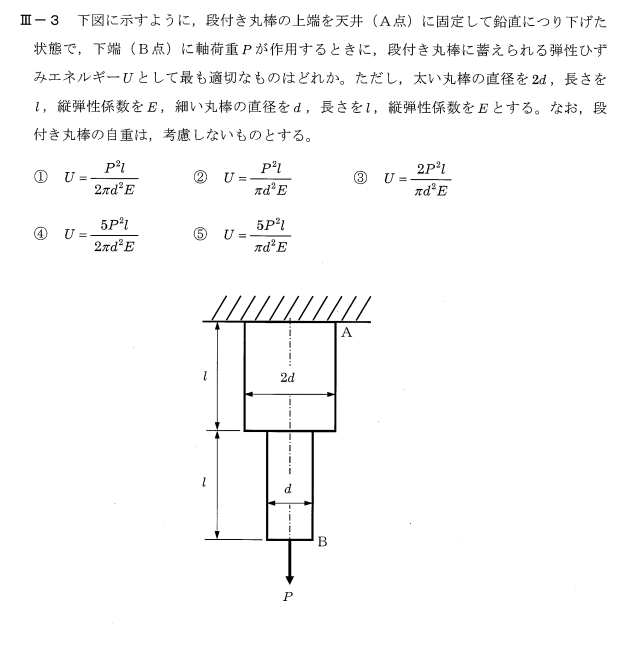
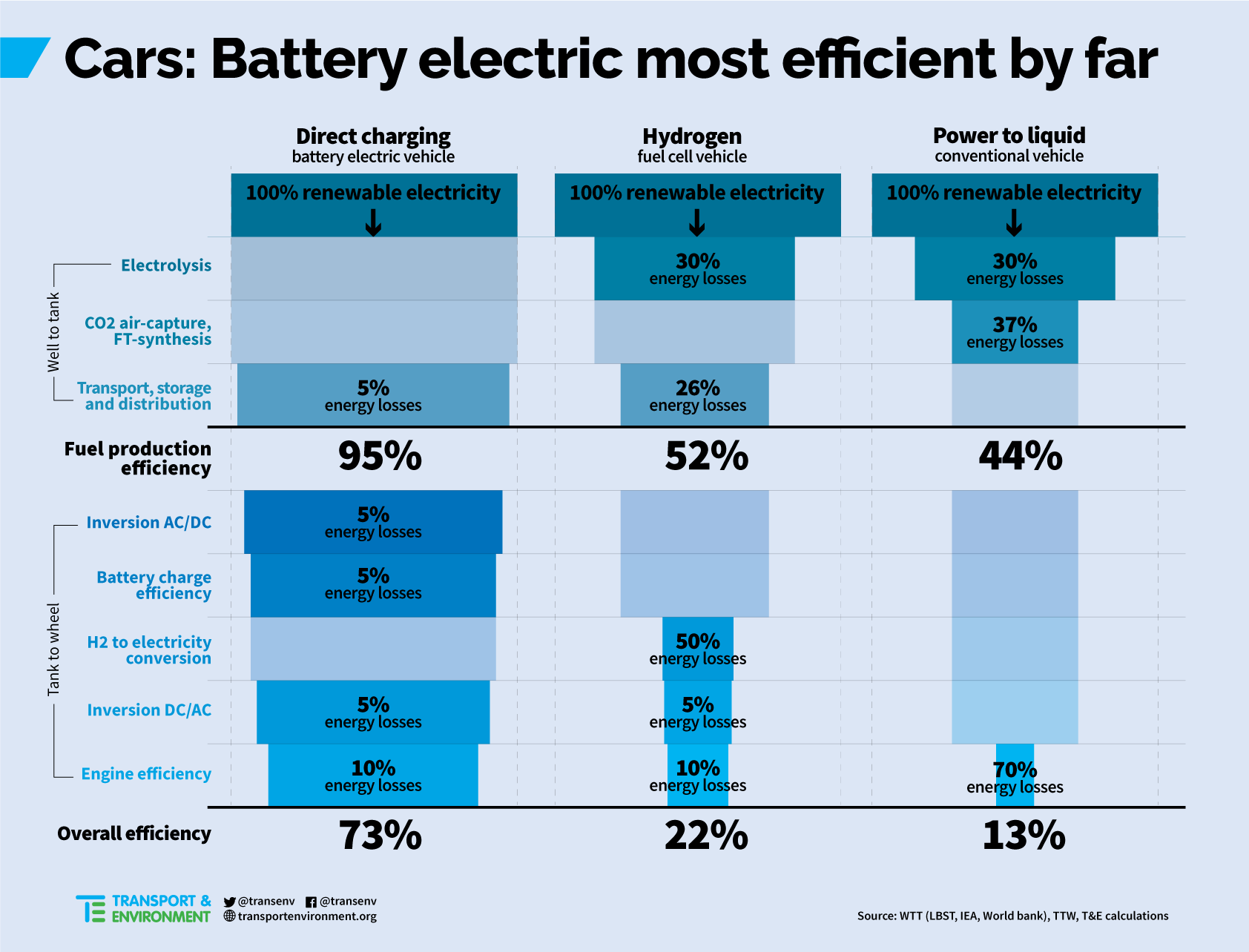
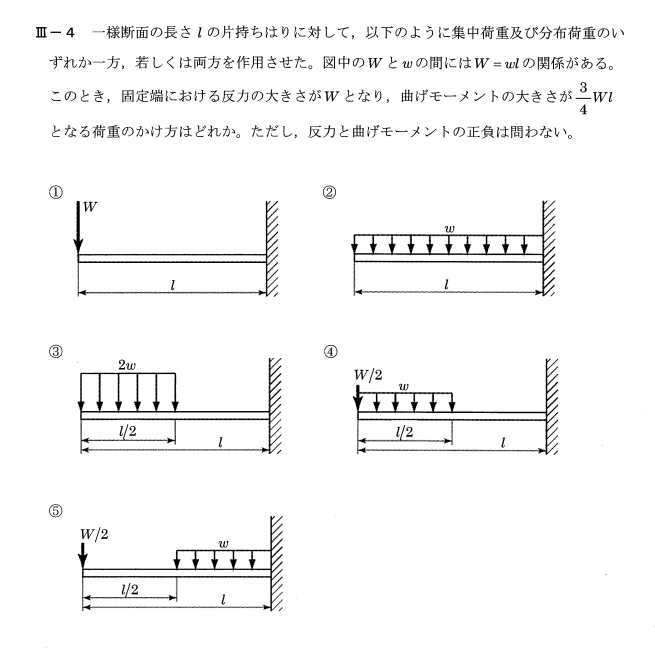
 それぞれのはりで反力Rをもとめる。
$R_1 = W$
$R_2 = wl = W$
$R_3 = 2w\frac{ l }{2} = W$
$R_4 = \frac{ W }{2} + w\frac{ l }{2} = W$
$R_5 = \frac{ W }{2} + w\frac{ l }{2} = W$
次に曲げモーメントを求める。
等分布荷重の場合、等分布荷重の中心位置に相当荷重がかかると置き換える事ができる。
$M_1 = Wl$
$M_2 = W・\frac{ l }{2}$
$M_3 = W・\frac{ 3l }{4}$
$M_4 = \frac{ W }{2}・\frac{ 3l }{4} + \frac{ W }{2}・l = \frac{ 7Wl }{8}$
$M_5 = \frac{ W }{2}・\frac{ l }{4} + \frac{ W }{2}・l = \frac{ 5Wl }{8}$
[解答] ③
参考:
それぞれのはりで反力Rをもとめる。
$R_1 = W$
$R_2 = wl = W$
$R_3 = 2w\frac{ l }{2} = W$
$R_4 = \frac{ W }{2} + w\frac{ l }{2} = W$
$R_5 = \frac{ W }{2} + w\frac{ l }{2} = W$
次に曲げモーメントを求める。
等分布荷重の場合、等分布荷重の中心位置に相当荷重がかかると置き換える事ができる。
$M_1 = Wl$
$M_2 = W・\frac{ l }{2}$
$M_3 = W・\frac{ 3l }{4}$
$M_4 = \frac{ W }{2}・\frac{ 3l }{4} + \frac{ W }{2}・l = \frac{ 7Wl }{8}$
$M_5 = \frac{ W }{2}・\frac{ l }{4} + \frac{ W }{2}・l = \frac{ 5Wl }{8}$
[解答] ③
参考:
平成25年度技術士第一次試験問題[機械部門] 専門科目Ⅲ-4 片持ち梁のたわみと曲げモーメント荷重の関係
 それぞれのはりで反力Rをもとめる。
$R_1 = W$
$R_2 = wl = W$
$R_3 = 2w\frac{ l }{2} = W$
$R_4 = \frac{ W }{2} + w\frac{ l }{2} = W$
$R_5 = \frac{ W }{2} + w\frac{ l }{2} = W$
次に曲げモーメントを求める。
等分布荷重の場合、等分布荷重の中心位置に相当荷重がかかると置き換える事ができる。
$M_1 = Wl$
$M_2 = W・\frac{ l }{2}$
$M_3 = W・\frac{ 3l }{4}$
$M_4 = \frac{ W }{2}・\frac{ 3l }{4} + \frac{ W }{2}・l = \frac{ 7Wl }{8}$
$M_5 = \frac{ W }{2}・\frac{ l }{4} + \frac{ W }{2}・l = \frac{ 5Wl }{8}$
[解答] ③
参考:
それぞれのはりで反力Rをもとめる。
$R_1 = W$
$R_2 = wl = W$
$R_3 = 2w\frac{ l }{2} = W$
$R_4 = \frac{ W }{2} + w\frac{ l }{2} = W$
$R_5 = \frac{ W }{2} + w\frac{ l }{2} = W$
次に曲げモーメントを求める。
等分布荷重の場合、等分布荷重の中心位置に相当荷重がかかると置き換える事ができる。
$M_1 = Wl$
$M_2 = W・\frac{ l }{2}$
$M_3 = W・\frac{ 3l }{4}$
$M_4 = \frac{ W }{2}・\frac{ 3l }{4} + \frac{ W }{2}・l = \frac{ 7Wl }{8}$
$M_5 = \frac{ W }{2}・\frac{ l }{4} + \frac{ W }{2}・l = \frac{ 5Wl }{8}$
[解答] ③
参考: