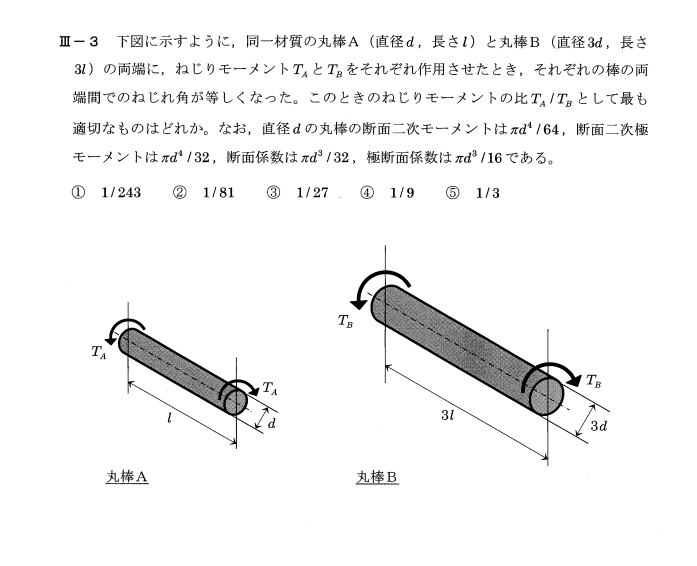
ねじりモーメントTに対するねじれ角φは、
$φ = \frac{ Tl }{ GI_P }$
従って丸棒Aのねじれ角は
$φ_A = \frac{ T_Al }{ GI_P } = \frac{ T_Al }{ G(\frac{ πd^4 }{ 32 }) } = \frac{ 32T_Al }{ πGｄ^4 }$
丸棒Bのねじれ角は
$φ_B = \frac{ T_B・3l }{ GI_P } = \frac{ T_B・3l }{ G(\frac{ π（3d）^4 }{ 32 }) }= \frac{ 32T_Bl }{27 πGｄ^4 } $
$φ_A = φ_B$であるから、
$\frac{ 32T_Al }{ πGｄ^4 } = \frac{ 32T_Bl }{27 πGｄ^4 }$
$\frac{ T_A }{T_B} =\frac{1}{27} $
参考：12.断面二次極モーメント｜材料力学
平成25年度技術士第一次試験問題［機械部門］ 専門科目Ⅲ-3 材料力学 丸棒の断面に働くねじりモーメントと断面係数に関する問題
- 更新日：
- 公開日：
ねじりモーメントTに対するねじれ角φは、
$φ = \frac{ Tl }{ GI_P }$
従って丸棒Aのねじれ角は
$φ_A = \frac{ T_Al }{ GI_P } = \frac{ T_Al }{ G(\frac{ πd^4 }{ 32 }) } = \frac{ 32T_Al }{ πGｄ^4 }$
丸棒Bのねじれ角は
$φ_B = \frac{ T_B・3l }{ GI_P } = \frac{ T_B・3l }{ G(\frac{ π（3d）^4 }{ 32 }) }= \frac{ 32T_Bl }{27 πGｄ^4 } $
$φ_A = φ_B$であるから、
$\frac{ 32T_Al }{ πGｄ^4 } = \frac{ 32T_Bl }{27 πGｄ^4 }$
$\frac{ T_A }{T_B} =\frac{1}{27} $
参考：12.断面二次極モーメント｜材料力学
