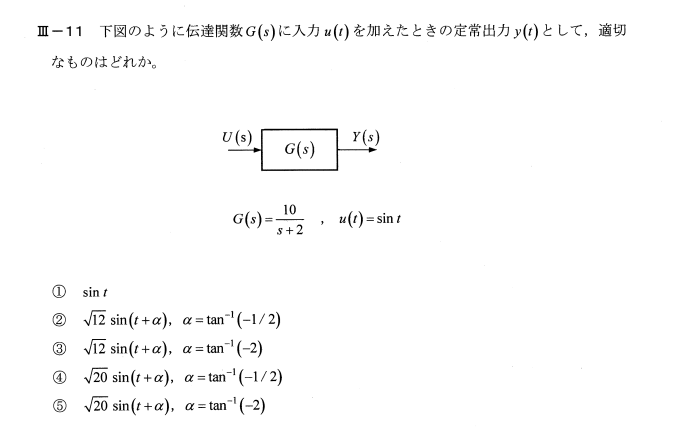
u(t)をラプラス変換してU(s)を求める
$L[ sint] = \frac{1}{s^2 + 1^2}$
設問図の入出力の関数より
$Y(s)=U(s)G(s)=\frac{1}{s^2 + 1^2}・\frac{10}{s + 2}=\frac{as+b}{s^2 + 1^2}+\frac{c}{s + 2}=\frac{-2s+4}{s^2 + 1^2}+\frac{2}{s + 2}$
逆ラプラス変換して
$y(t)=L^{-1}[ Y(s)] = -2cost + 4sint +2e^{-2t}$
ここで定常出力（t→∞）では$2e^{-2t}→0$となることと三角関数の公式を用いて
$y(t)=\sqrt{20}sin(t+tan^{-1}(-1/2)) $
[解答]④
参考
ラプラス変換とラプラス逆変換(H26)
ラプラス変換 例題(H25)
令和3年度技術士第一次試験問題［機械部門］ 専門科目Ⅲ-11 ラプラス変換と伝達関数
- 公開日：
u(t)をラプラス変換してU(s)を求める
$L[ sint] = \frac{1}{s^2 + 1^2}$
設問図の入出力の関数より
$Y(s)=U(s)G(s)=\frac{1}{s^2 + 1^2}・\frac{10}{s + 2}=\frac{as+b}{s^2 + 1^2}+\frac{c}{s + 2}=\frac{-2s+4}{s^2 + 1^2}+\frac{2}{s + 2}$
逆ラプラス変換して
$y(t)=L^{-1}[ Y(s)] = -2cost + 4sint +2e^{-2t}$
ここで定常出力（t→∞）では$2e^{-2t}→0$となることと三角関数の公式を用いて
$y(t)=\sqrt{20}sin(t+tan^{-1}(-1/2)) $
[解答]④
参考
ラプラス変換とラプラス逆変換(H26)
ラプラス変換 例題(H25)
