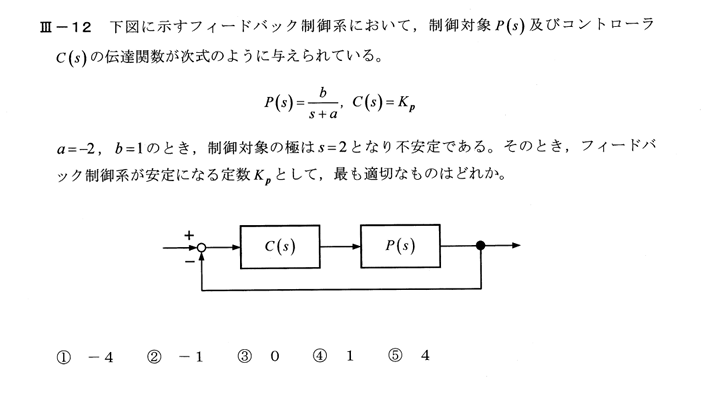
図より、伝達関数は
$ \frac{C(s)P(s)}{ 1+C(s)P(s) } =\frac{\frac{K_p}{ s-2 }}{ 1+\frac{K_p}{ s-2 } } =\frac{K_p}{ s-2+K_p } $
となる。この系が安定となるためには、フルビッツの方法を適用して
$K_ｐ＞０ $、$K_ｐ-2＞０ $であるため
[解答]⑤
参考
フィードバック制御系の安定性（H26）
フルビッツの安定判別法
安定条件について教えて下さい
安定条件を
いちばん本質的なところから わかりやすく説明します。
ここでは
- なぜ極が左半平面なら安定？
- 右半平面ならなぜ不安定？
- 境界はどこ？
- 今回の問題ではどう判断する？
を、丁寧に整理します。
✅ 1. 安定条件の基本（最重要）
連続時間システムは、すべての極が左半平面（Re(s)<0）にあれば安定。
逆に、
- 極が右半平面（Re(s)>0）にあれば不安定
- 極が虚軸上にある場合も基本的に“不安定扱い” or “安定とは言えない”
これは
e^{st} の性質 から決まる。
✅ 2. なぜ極の位置で安定が決まるのか？
システムの時間応答は
[
e^{st}
]
の形を含む。
たとえば 1 次系なら
[
G(s)=\frac{1}{s+3} \quad\Rightarrow\quad y(t)=1-e^{-3t}
]
ここで、指数関数の振る舞いを見ると
| (s) の実部 |
挙動 |
| (s<0) |
(e^{st} = e^{- |
| (s=0) |
(e^{0t}=1) → 収束しない（不安定） |
| (s>0) |
(e^{st}=e^{+ |
つまり：
✅
安定にするためには s の実部が負である必要がある
✅ 3. 多次系でも同じ（極の集合で決まる）
伝達関数の極が
[
s = p_1, p_2, \dots
]
とすると、
- 1つでも Re(p_i) > 0 の極がある → 不安定
- 全部 Re(p_i) < 0 → 安定
✅ 4. 今回の問題の安定条件
閉ループ伝達関数の極は
[
s = 2 - K_p
]
この極が左側（負の実部）に来ればよい。
[
2-K_p < 0
]
[
K_p > 2
]
これが
安定条件。
✅ 5. なぜ Kp > 2 で安定になるのか？（物理的解釈）
元の制御対象の極は
s = 2（右半平面）
→ これは不安定な系（指数的に発散する）
負帰還をかけると閉ループ極は
[
s = 2 - K_p
]
- Kp を 0 のまま → s=2 → 発散（不安定）
- Kp を 2 にする → s=0 → 発散（不安定）
- Kp を 3 にする → s = −1 → 安定！
- Kp を 4 にする → s = −2 → より安定
つまり Kp を大きくすると
負の方向に極が押し込まれていく＝安定化される。
✅ 6. 安定条件まとめ（覚え方）
| 条件 |
意味 |
| Re（極） < 0 |
安定 |
| Re（極） = 0 |
不安定（発散 or 収束せず） |
| Re（極） > 0 |
完全に不安定 |
✅ 7. まとめ（今回の答えに戻る）
閉ループ極
[
s = 2 - K_p
]
安定条件
[
2 - K_p < 0 \quad\Rightarrow\quad K_p > 2
]
選択肢の中で最も適切なのは
✅
Kp = 4（⑤）
必要であれば：
✅ 判別式を使う安定判定（2次多項式）
✅ ラウス・フルビッツ（3次以上）
✅ 根軌跡での視覚的理解
✅ PID の場合の安定条件
なども詳しく説明できます！
たとえば 1 次系なら G(s)=\frac{1}{s+3} \quad\Rightarrow\quad y(t)=1-e^{-3t} のGsやytはなんですか？
とても良い質問です。「(G(s)) や (y(t)) ってそもそも何？」というところをしっかり整理すると、制御工学が一気にわかりやすくなります。
以下、
意味 → 役割 → なぜそう書くのか の順で説明します。
✅ 1. (G(s)) とは何か？
伝達関数（Transfer Function）です。
システムの「入力 → 出力」の関係を
ラプラス領域で表した関数。
たとえば
[
G(s)=\frac{1}{s+3}
]
これは、時間領域で見ると
[
\dot{y}(t)+3y(t)=u(t)
]
という1次遅れ微分方程式に対応します。
✅ なぜラプラス領域で書くの？
- 微分方程式が 代数式になる
- 畳み込み（応答計算）が 掛け算になる
- 安定性が 極を見るだけでわかる
だから制御では
G(s) を使うのが基本。
✅ 2. (y(t)) とは何か？
出力の時間応答（時間領域）です。
時間 t が増えるとき、出力がどう変化するかという「現実の信号」。
例：
[
y(t)=1-e^{-3t}
]
これは「ステップ入力を加えたときの実際の応答」を表します。
- (t=0) 付近では 0
- (t\to\infty) で 1 に近づく
典型的な
1次遅れ応答 の形。
✅ 3. G(s) と y(t) は「世界が違う」
| 記号 |
どこの世界？ |
意味 |
| (G(s)) |
s 領域（ラプラス領域） |
システムの性質（伝達関数） |
| (Y(s)) |
s 領域 |
出力のラプラス変換 |
| (y(t)) |
時間領域 |
現実の時間応答 |
つまり、
- G(s) は「システムを数学的に表したもの」
- y(t) は「実際の出力（時間の信号）」
✅ 4. 例：1次系のステップ応答
伝達関数
[
G(s)=\frac{1}{s+3}
]
ステップ入力を入れると (R(s)=1/s)
[
Y(s)=G(s)R(s)=\frac{1}{s(s+3)}
]
部分分解して逆ラプラス変換すると：
[
y(t)=1-e^{-3t}
]
✅ ここでの意味
- G(s) → システムの性質
- y(t) → 実際に観測される出力の時間変化
✅ 5. なんで G(s) と y(t) を混ぜて出すの？
時間応答を求める流れが：
- システムの伝達関数 G(s) を使い
- 入力 R(s) と掛けて Y(s) を求め
- 逆ラプラス変換して y(t) を得る
というプロセスだからです。
✅ 最後に一言でまとめると
- G(s) はシステムの「性格表」
- y(t) はそのシステムが実際に「どう動いたか」
という
別世界の値。
制御ではこの2つを行き来しながら解析します。
もしよければ、
✅ Y(s) と y(t) の対応（逆ラプラスの仕組み）
✅ 1次系の応答をグラフで見たい
✅ 2次系のステップ応答も見たい
なども続けて説明できます！
時間領域で見ると一次方程式は1次遅れなの？
結論から言うと
「時間領域での一次方程式（1階微分方程式）＝1次遅れ系」 です。
ただし、正確には
“安定な一次系” の場合に 1次遅れになる ので、その意味も含めて丁寧に説明します。
✅ 1. そもそも「1次遅れ」とは？
時間応答が
[
y(t)=y(\infty)\left(1-e^{-t/T}\right)
]
の形になる系。
特徴：
- 立ち上がりがゆっくり
- 時間定数 (T) (=1/極の絶対値) を持つ
- ステップ応答が指数関数的に収束する
工学では「1次遅れ」、「一次応答」と呼ぶ。
✅ 2. WHY：なぜ 1階微分方程式は 1次遅れなの？
1階微分方程式
[
\dot y(t) + a y(t)= b u(t)
]
これをラプラス変換すると
[
(s+a)Y(s)=\frac{b}{s}
]
よって
[
G(s)=\frac{Y(s)}{U(s)}=\frac{b}{s+a}
]
これは
右半平面に極を1つ持つ 1次系（一次遅れ系） の標準形。
✅ 3. 逆ラプラスして時間領域へ戻すと…
ステップ入力 (u(t)=1) なら
[
Y(s)=\frac{b}{s(s+a)}
]
逆ラプラスすると
[
y(t)=\frac{b}{a}\left(1-e^{-at}\right)
]
これは典型的な
1次遅れ応答。
✅ 4. 一次“遅れ”という名前がつく理由
この式
[
y(t) = 1 - e^{-at}
]
は
- 入力を「パッと」変えても
- 出力が「遅れて」ついてくる
- その遅れ具合が指数関数的
だから “遅れる” →
1次遅れ系 と呼ばれる。
✅ 5. ただし注意！
✅ 安定な場合だけ「1次遅れ」と呼べる
極 (-a) が左側にある（a>0）
→ 収束 → 1次遅れ
❌ 極が右半平面（a<0）
[
y(t)=1-e^{+|a|t}
]
→ 発散
→
不安定一次系
→ 1次遅れとは言わない
なので、
- 安定な一次微分方程式 → 一次遅れ系
- 不安定な一次微分方程式 → 一次発散系
となる。
✅ 6. まとめ（シンプル版）
| 時間領域の形 |
s領域の形 |
呼び名 |
| (\dot y + a y = b u) |
(G(s)=\frac{b}{s+a}) |
一次遅れ系（a>0） |
| 同じ |
極が正の位置 |
不安定一次系 |
✅ 7. さらに深い理解：極の個数=微分方程式の次数
1次微分方程式 → 極が1個 → 一次遅れ系
2次微分方程式 → 極が2個 → 2次振動系
この対応が制御工学の根本。
必要なら：
✅ 1次遅れと 2次遅れの違い
✅ 時定数 (T) の意味
✅ 応答のグラフ（図で分かりやすく）
✅ 不安定一次系の挙動
などもさらに深く説明できます！
