令和3年度技術士第一次試験問題［機械部門］　専門科目Ⅲ-5　片持ち梁のたわみ

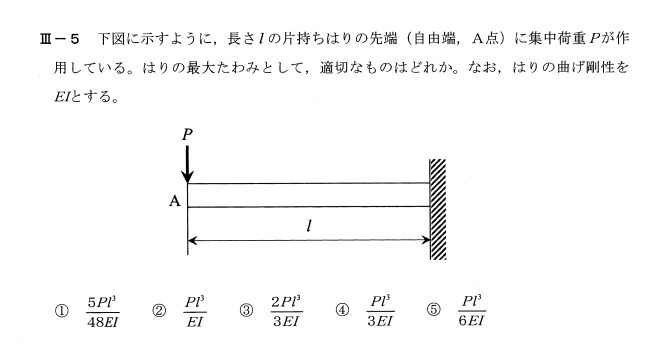
荷重Pがかかる梁のたわみは
$\frac{ d^{2}y }{ dx^2 } = -\frac{ M(x) }{ EI }= -\frac{ P(l-x) }{ EI }$

となる。

上式を積分して、

$\frac{ dy }{ dx } = -\frac{ P}{ EI }(lx+\frac{ x^2}{ 2 }) + C_1$

さらに積分して

$ｙ = -\frac{ P}{ EI }(\frac{ lx^2}{ 2 }+\frac{ x^3}{ 6 }) + C_{1}x + C_2$

ここで梁の境界条件

ｘ＝0のとき、ｙ＝0
ｘ＝0のとき、$\frac{ dy }{ dx } = 0$

より、$C_1 = 0、C_2 =  0$

よって、

$ｙ = -\frac{ P}{ EI }(\frac{ lx^2}{ 2 }+\frac{ x^3}{ 6 })$

ｘ＝ｌのときにたわみが最大となるので、代入して整理すると

$ｙ = \frac{ Pl^3}{ 3EI }$

[解答] ③

参考

第9回　不静定はりのたわみ

平成25年度技術士第一次試験問題［機械部門］　専門科目Ⅲ-6　材料力学 両端支持梁のたわみ