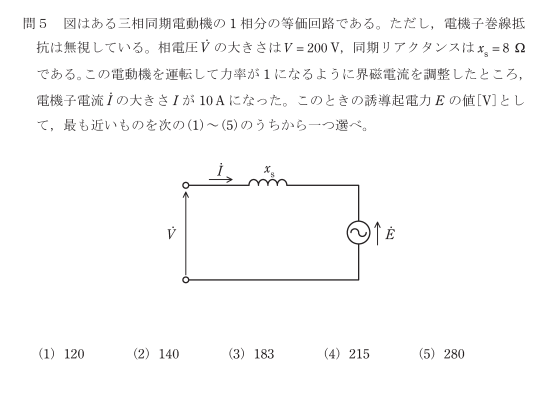
平成26年度技術士第一次試験問題［機械部門］　専門科目Ⅲ-12 図より、伝達関数は $　\frac{C(s)P(s)}{ 1+C(s)P(s) } =\frac{\frac{K_p}{ s-2 }}{ 1+\frac{K_p}{ s-2 } } =\frac{K_p}{ s-2+K_p } $ となる。この系が安定となるためには、フルビッツの方法を適用して $K_ｐ＞０ $、$K_ｐ-2＞０ $であるため [解答]④ [参考] 特性方程式（つまり伝達関数の分母）の中で、sに付いている係数が1つでも負であれば、そのシステムは不安定であることが知られています。 ただし、この判別基準は不安定性の十分条件に過ぎないため注意が必要です。つまり、sに付いている係数がすべて正であっても、そのシステムは安定とは言えません。 特性方程式の係数が1つでも負 ⇒ 絶対に不安定 特性方程式の係数が全て正 ⇒ 安定性・不安定どちらもありうる   慶應大学講義　制御工学同演習第九回　フィードバック制御系２,安定性１ 第 10 単元 Hurwitz の安定性判別法 安定判別はフルビッツの安定判別法が簡単 平成25年度技術士第一次試験問題［機械部門］　専門科目Ⅲ-11　フィードバック制御系の伝達関数の求め方 平成25年度技術士第一次試験問題［機械部門］　専門科目Ⅲ-12　フィードバック制御 伝達関数 ブロック線図の等価変換や簡略化