断面係数 $Z$ は両者で等しいので，最大応力度 $$\sigma_{\max}=\frac{M_{\max}}{Z}$$   を比較するには，最大曲げモーメント $M_{\max}$ を比べればよい．

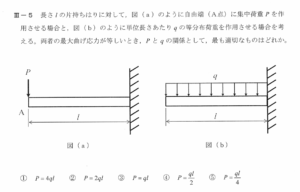
1. 図(a)（集中荷重 $P$  ）の最大曲げモーメント $M_a = P \times l$ 
2. 図(b)（等分布荷重 $q$  ）の合力は $q\,l$  ，作用位置は支点から $l/2$  $$M_b = (q\,l)\times\frac{l}{2} = \frac{q\,l^2}{2}$$ 

これらを等しいとおくと， $$P\,l = \frac{q\,l^2}{2} \quad\Longrightarrow\quad P = \frac{q\,l}{2}$$   したがって，最も適切なのは $$\boxed{P = \frac{q\,l}{2}}$$   すなわち選択肢④．   参考：技術士第一次試験－令和2年度機械部門Ⅲ-5解答例 | 技術士のたまご  

断面係数の定義を教えて下さい

断面係数（Section Modulus, 記号 Z）の定義は、 部材の曲げに対する強さを表す断面形状の指標であり、

---

■ 断面係数の定義（最重要）

[ \boxed{Z = \frac{I}{c}} ] ここで

記号	意味
(I)	中立軸まわりの断面二次モーメント（moment of inertia）
(c)	中立軸から最外繊維までの距離（＝張力側・圧縮側の外端まで）

---

■ なぜ重要？

最大曲げ応力は： [ \boxed{\sigma_{\max} = \frac{M_{\max}}{Z}} ] となるため、 Z が大きいほど曲げに強い（＝同じ曲げモーメントでも応力が小さくなる）

---

■ 物理的な意味

断面係数 Z は、

• 断面形状が持つ「曲げに耐える能力」
• 断面の外側に材料がどれだけあるか

を表します。

---

■ 例

● 長方形断面（幅 b、高さ h）

[ I = \frac{b h^3}{12} ] [ Z = \frac{b h^2}{6} ] →高さ (h) を大きくすると Z が急激に増える （＝縦を高くしたH形鋼が強い理由）

---

● 円形断面（直径 d）

[ I=\frac{\pi d^4}{64} ] [ Z=\frac{\pi d^3}{32} ]

---

---

■まとめ

断面係数 (Z) とは： [ \boxed{Z = \frac{I}{c}} ]

---

必要なら、

• 導出の理解
• 直感的説明
• 断面二次モーメントとの違い
• 種類別のZ一覧表（H形鋼、L形鋼等）

などもお作りしますのでどうぞ。