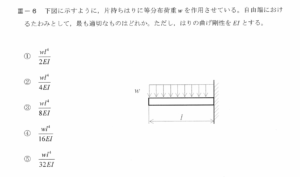
解答

自由端のたわみ

$$\boxed{\displaystyle \frac{w\,l^{4}}{8EI}}$$

よって ③ が最も適切です。

導出（片持ちはり・等分布荷重）

1. 座標系
   固定端を $x=0$ 

   、自由端を

   $x=l$ 

   とする。荷重

   $w\,[\text{N/m}]$ 

   は下向きに一様に作用。

2. せん断力
   $V(x)$ 

   $$V(x)=w(l-x)$$ 

3. 曲げモーメント
   $M(x)$ 

   せん断の積分

   $$M(x)=\int V(x)\,dx = \frac{w}{2}(l-x)^2$$（下向き荷重を負符号で取る流儀もあるが、符号は一貫していればよい。）

4. たわみ微分方程式
   $$EI\,\frac{d^2y}{dx^2}=M(x)=\frac{w}{2}(l-x)^2$$ 
5. 角度（傾き）
   $\theta(x)=dy/dx$ 

   $$EI\,\theta(x)=\int_0^{x}\frac{w}{2}(l-\xi)^2\,d\xi =\frac{w}{2}\left[l^2x-\!l x^2+\frac{x^3}{3}\right]$$ 

6. たわみ
   $y(x)$ 

   $$EI\,y(x)=\int_0^{x}EI\,\theta(\eta)\,d\eta =\frac{w}{2}\left[\frac{l^2x^{2}}{2}-\frac{l x^{3}}{3}+\frac{x^{4}}{12}\right]$$ 

7. 境界条件
   固定端で $y(0)=0,\;\theta(0)=0$ 

   を満たしているので積分定数は不要。

8. 自由端（
   $x=l$ 

   ）のたわみ

   $$y(l)=\frac{w}{2EI}\left[\frac{l^4}{2}-\frac{l^4}{3}+\frac{l^4}{12}\right] =\frac{w\,l^{4}}{8EI}$$ 

参考式（覚えておくと便利）

（本問は下段のケース）

参考：技術士第一次試験－令和2年度機械部門Ⅲ-6解答例 | 技術士のたまご

曲げモーメントはせん断の積分なのですか？距離×せん断ではないですか？

せん断力 $V$ と曲げモーメント $M$ の関係は

$$\boxed{\dfrac{dM}{dx}=V(x)}$$

1. 微小要素のつり合いから導くと

片持ちはりの任意断面で幅 $dx$ の微小片を取り、鉛直方向とモーメントのつり合いを書きます。

したがって せん断力はモーメントの空間微分、逆に

$$M(x)=\int V(x)\,dx + C$$

となります。

2. 「せん断×距離」と「積分」の関係

• せん断が区間内で一定（＝点荷重 $P$ だけが掛かっている区間など）
  $V(x)=P$ が定数なので

  $$M(x)=\int P\,dx = P\,x + C \quad\Longrightarrow\quad \text{“せん断（=P）×距離（=x）”}$$つまり 「せん断×距離」 は「積分」の特殊ケースです。

• せん断が位置によって変わる（等分布荷重など）
  例：片持ちはりに一様荷重 $w$

  $$V(x)=w(l-x) \quad(\text{右側の荷重の合力})$$は $x$ の一次関数なので

  $$M(x)=\int_0^{x}w(l-\xi)\,d\xi=\frac{w}{2}(l-x)^2\;(＋C)$$となり、単純に「せん断×距離」では表せません。

3. イメージしやすい整理

まとめ

• 一般には　$M(x)=\displaystyle\int V(x)\,dx$
• せん断が一定の区間だけ　→ 「せん断×距離」がその積分結果と一致するだけ

したがってご質問の

曲げモーメントはせん断の積分なのですか？距離×せん断ではないですか？

という疑問は、

1. “積分” が本質的な一般式
2. “せん断×距離” は せん断が一定の場合に限り その積分が簡単な形で表れる特別ケース

という二段構えで整理するとスッキリします。