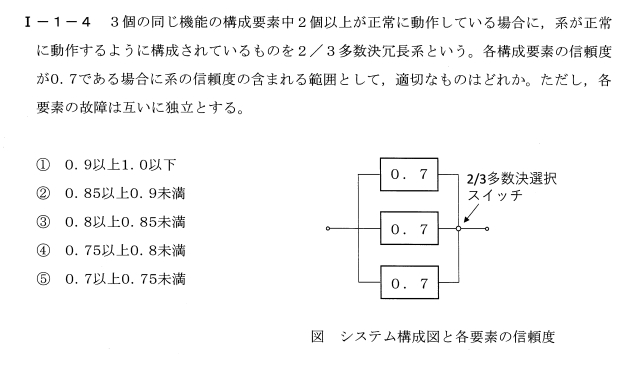
 この問題では、3つの構成要素のうち2つ以上が正常に動作する場合に系が正常に動作する「2/3多数決冗長系」の信頼度を求める必要があります。各構成要素の信頼度は0.7であり、故障は互いに独立です。
まず、系の信頼度を求めるために、以下の状況を考えます。
1. 3つの構成要素がすべて正常に動作する場合。
2. 3つの構成要素のうち2つが正常に動作する場合。
各構成要素の信頼度が0.7であることから、故障する確率は0.3です。
1. **すべての構成要素が正常に動作する確率:**
\[ P(3) = 0.7 \times 0.7 \times 0.7 = 0.343 \]
2. **3つの構成要素のうち2つが正常に動作する確率:**
構成要素のうち2つが正常で1つが故障する確率を求めます。この場合、次の3通りの組み合わせがあります。
- 正常, 正常, 故障
- 正常, 故障, 正常
- 故障, 正常, 正常
それぞれの確率は次のように計算されます:
\[ P(2) = 3 \times (0.7 \times 0.7 \times 0.3) = 3 \times 0.147 = 0.441 \]
最後に、これらの確率を合計します。
\[ P(系の信頼度) = P(3) + P(2) = 0.343 + 0.441 = 0.784 \]
したがって、系の信頼度は0.784となり、この値が含まれる範囲は選択肢の中で **「0.75以上0.8未満」** です。
**正解は 4. 0.75以上0.8未満** です。
[解答]④
この問題では、3つの構成要素のうち2つ以上が正常に動作する場合に系が正常に動作する「2/3多数決冗長系」の信頼度を求める必要があります。各構成要素の信頼度は0.7であり、故障は互いに独立です。
まず、系の信頼度を求めるために、以下の状況を考えます。
1. 3つの構成要素がすべて正常に動作する場合。
2. 3つの構成要素のうち2つが正常に動作する場合。
各構成要素の信頼度が0.7であることから、故障する確率は0.3です。
1. **すべての構成要素が正常に動作する確率:**
\[ P(3) = 0.7 \times 0.7 \times 0.7 = 0.343 \]
2. **3つの構成要素のうち2つが正常に動作する確率:**
構成要素のうち2つが正常で1つが故障する確率を求めます。この場合、次の3通りの組み合わせがあります。
- 正常, 正常, 故障
- 正常, 故障, 正常
- 故障, 正常, 正常
それぞれの確率は次のように計算されます:
\[ P(2) = 3 \times (0.7 \times 0.7 \times 0.3) = 3 \times 0.147 = 0.441 \]
最後に、これらの確率を合計します。
\[ P(系の信頼度) = P(3) + P(2) = 0.343 + 0.441 = 0.784 \]
したがって、系の信頼度は0.784となり、この値が含まれる範囲は選択肢の中で **「0.75以上0.8未満」** です。
**正解は 4. 0.75以上0.8未満** です。
[解答]④
令和5年度技術士第一次試験問題[基礎科目] 問Ⅰ-1-4 2/3多数決冗長系の信頼度を求める
 この問題では、3つの構成要素のうち2つ以上が正常に動作する場合に系が正常に動作する「2/3多数決冗長系」の信頼度を求める必要があります。各構成要素の信頼度は0.7であり、故障は互いに独立です。
まず、系の信頼度を求めるために、以下の状況を考えます。
1. 3つの構成要素がすべて正常に動作する場合。
2. 3つの構成要素のうち2つが正常に動作する場合。
各構成要素の信頼度が0.7であることから、故障する確率は0.3です。
1. **すべての構成要素が正常に動作する確率:**
\[ P(3) = 0.7 \times 0.7 \times 0.7 = 0.343 \]
2. **3つの構成要素のうち2つが正常に動作する確率:**
構成要素のうち2つが正常で1つが故障する確率を求めます。この場合、次の3通りの組み合わせがあります。
- 正常, 正常, 故障
- 正常, 故障, 正常
- 故障, 正常, 正常
それぞれの確率は次のように計算されます:
\[ P(2) = 3 \times (0.7 \times 0.7 \times 0.3) = 3 \times 0.147 = 0.441 \]
最後に、これらの確率を合計します。
\[ P(系の信頼度) = P(3) + P(2) = 0.343 + 0.441 = 0.784 \]
したがって、系の信頼度は0.784となり、この値が含まれる範囲は選択肢の中で **「0.75以上0.8未満」** です。
**正解は 4. 0.75以上0.8未満** です。
[解答]④
この問題では、3つの構成要素のうち2つ以上が正常に動作する場合に系が正常に動作する「2/3多数決冗長系」の信頼度を求める必要があります。各構成要素の信頼度は0.7であり、故障は互いに独立です。
まず、系の信頼度を求めるために、以下の状況を考えます。
1. 3つの構成要素がすべて正常に動作する場合。
2. 3つの構成要素のうち2つが正常に動作する場合。
各構成要素の信頼度が0.7であることから、故障する確率は0.3です。
1. **すべての構成要素が正常に動作する確率:**
\[ P(3) = 0.7 \times 0.7 \times 0.7 = 0.343 \]
2. **3つの構成要素のうち2つが正常に動作する確率:**
構成要素のうち2つが正常で1つが故障する確率を求めます。この場合、次の3通りの組み合わせがあります。
- 正常, 正常, 故障
- 正常, 故障, 正常
- 故障, 正常, 正常
それぞれの確率は次のように計算されます:
\[ P(2) = 3 \times (0.7 \times 0.7 \times 0.3) = 3 \times 0.147 = 0.441 \]
最後に、これらの確率を合計します。
\[ P(系の信頼度) = P(3) + P(2) = 0.343 + 0.441 = 0.784 \]
したがって、系の信頼度は0.784となり、この値が含まれる範囲は選択肢の中で **「0.75以上0.8未満」** です。
**正解は 4. 0.75以上0.8未満** です。
[解答]④




