求めるのは領域 (C) の循環
[
\Gamma=\oint_{\partial C}\mathbf{v}\cdot d\mathbf{l}
]
です。
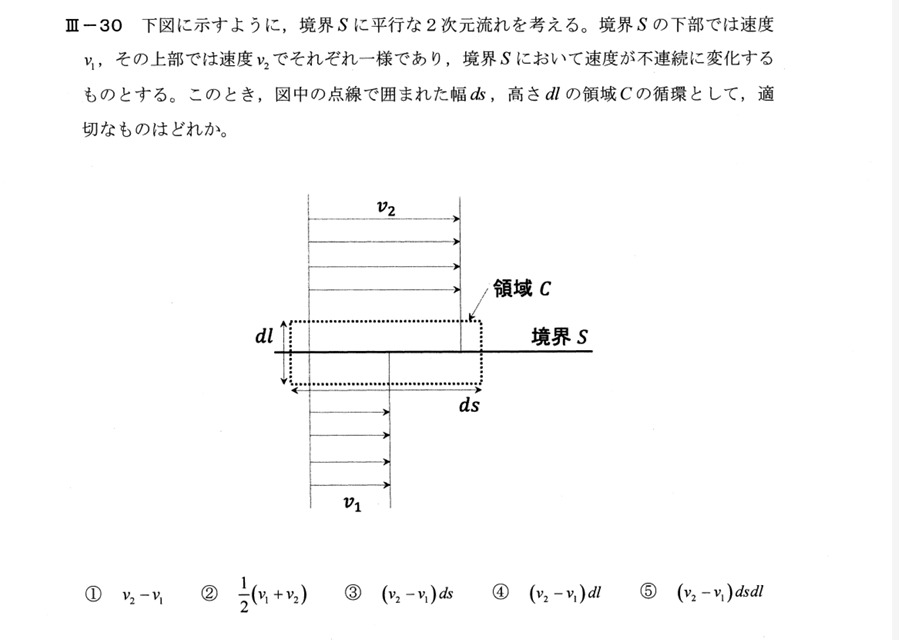
- 流れは境界 (S) の上下で一様：下側で (v_1)，上側で (v_2)。いずれも水平方向。
- 積分経路は図の細長い長方形（幅 (ds)，高さ (dl)）の外周。
- 上辺（長さ (ds)）は上流域にあり、[\mathbf{v}=v_2] が進行方向と同向 → 寄与 [= v_2,ds]。
- 下辺（長さ (ds)）は下流域にあり、[\mathbf{v}=v_1] は上辺と同じ向きだが、線素の向きは周回方向と逆向き → 寄与 [= -,v_1,ds]。
- 左右の辺は鉛直で、速度は水平方向なので [\mathbf{v}\cdot d\mathbf{l}=0] で寄与なし。
循環とはなんですか
**循環（circulation）**とは、流体がある閉じた経路に沿ってどれだけ「回っているか」を表す量で、速度ベクトルを経路に沿って積分したものです。■ 定義式
閉曲線 (C) に沿う循環 (\Gamma) は [ \Gamma = \oint_C \mathbf{v}\cdot d\mathbf{l} ]- (\mathbf{v})：流体の速度ベクトル
- (d\mathbf{l})：経路に沿った微小線素
- 積分は閉曲線（ぐるっと一周）
流体が閉ループにそってどれくらい渦のように動いているかを表す量です。
■ 直感的イメージ
- 静止流体では循環 = 0
- 均一にまっすぐ流れている流れでも循環 = 0 （左右対称に打ち消し合う）
- 渦（回転流）では循環 ≠ 0
■ 渦度との関係
循環は渦度 (\omega)と密接です。 [ \Gamma = \iint_S \omega, dS ] 渦度は「局所的な回り」の指標、 循環はそれを面で積分した「全体の回り具合」。■ 例：川の流れ vs 渦
| 流れ | 循環 |
|---|---|
| まっすぐ流れる川 | 0（回転していない） |
| 渦巻き流れ | 大きい（ぐるぐる回る） |
■ なぜ重要？
流体力学で循環は多くの法則と関係します：- クッタ–ジュコフスキーの揚力公式 [ L' = \rho U \Gamma ]
- 渦度輸送方程式
- ケルビンの循環定理
■ まとめ
| 項目 | 内容 |
|---|---|
| 循環 | 閉経路に沿う速度成分の積分 |
| 意味 | 流れの「ぐるぐる具合」を表す |
| 式 | [\Gamma = \oint \mathbf{v}\cdot d\mathbf{l}] |
| 渦との関係 | 渦度の面積積分 |
| 例 | 渦のある流れでは循環 ≠ 0 |
必要なら、簡単な数値例や、翼断面まわりの循環図も作ります。 次にケルビンの循環定理や揚力との関係を解説しましょうか？ v・dlは内積ですか？ はい、([\mathbf{v} \cdot d\mathbf{l} ] は**内積（dot product）**です。
■ 意味
[ \mathbf{v} \cdot d\mathbf{l} = |\mathbf{v}|,|d\mathbf{l}| \cos\theta ]- [\mathbf{v}]：流速ベクトル
- [d\mathbf{l}]：線要素ベクトル（積分経路の向き）
- [\theta]：両ベクトルの角度
経路方向にどれだけ速度成分があるかを表しています。 速度が経路と同じ方向→正 逆向き→負 直交→0
■ 直感例
- 同じ方向に流れている水は、経路に沿って前進 → 正の寄与
- 逆向きだと負の寄与
- 直角方向の流れは循環には関係なし
■ 循環への関係
循環は [ \Gamma = \oint_C \mathbf{v} \cdot d\mathbf{l} ] ですから、 閉曲線に沿った速度の“向きあり”線積分になります。流れがぐるっと回るほど内積積分が大きくなる → 循環が大きい
■ 補足：なぜ内積？
循環は「回転量」の指標ですが、まずは- 経路に沿った速度成分（内積）
- それを経路に沿って積分
✅結論
(v\cdot dl) は内積です。 流れの「経路方向成分」を積分して循環を求めています。
さらに理解を深めたいなら
- 流線と循環
- Stokes の定理とのつながり
- 揚力（循環理論）
