運動方程式は
$ ｍ\frac{ d^2x_1 }{dt^2} + 2kx_1 - kx_2 = 0$
$ ｍ\frac{ d^2x_2 }{dt^2} + k_2(x_2 - x_1)= 0$
と書ける。
ここで、
x1=X1cosωt
x2=X2cosωt
と仮定しこれを満たす、振動数方程式を導出すると
$\begin{vmatrix}
-mω^2+2k & -k \\
-k & k -mω^2
\end{vmatrix}=0$
これを展開して、
$ ｍ^2ω^4-3mkω^2 + k^2 = 0$
[解答]④
参考：二自由度系の振動(3)
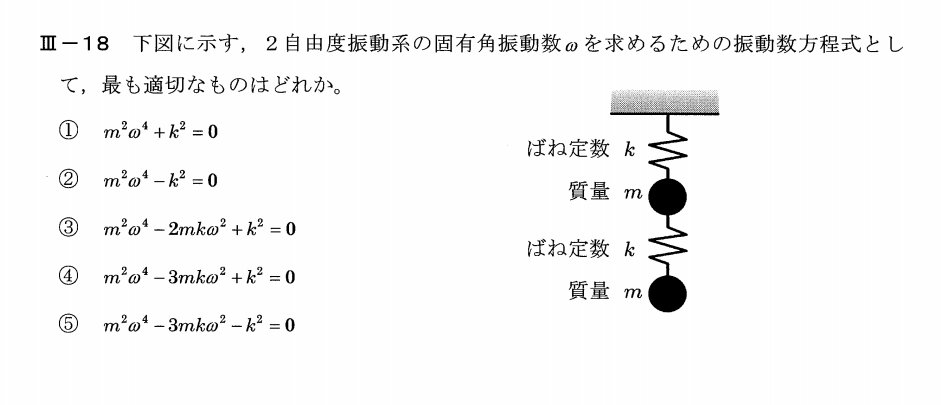
平成25年度技術士第一次試験問題［機械部門］ 専門科目Ⅲ-18 2自由度振動系の状態方程式
- 更新日：
- 公開日：
運動方程式は
$ ｍ\frac{ d^2x_1 }{dt^2} + 2kx_1 - kx_2 = 0$
$ ｍ\frac{ d^2x_2 }{dt^2} + k_2(x_2 - x_1)= 0$
と書ける。
ここで、
x1=X1cosωt
x2=X2cosωt
と仮定しこれを満たす、振動数方程式を導出すると
$\begin{vmatrix}
-mω^2+2k & -k \\
-k & k -mω^2
\end{vmatrix}=0$
これを展開して、
$ ｍ^2ω^4-3mkω^2 + k^2 = 0$
[解答]④
参考：二自由度系の振動(3)
