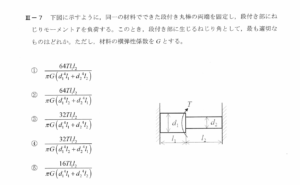
1. 反力トルクの求め方

中央（段付き部）に外力トルク

$T$

を加えると，左右のシャフトはそれぞれ

• 左側（長さ
  $l_1$ 

  ，直径 $d_1$ 

  ）に反力トルク $T_1$ 

• 右側（長さ
  $l_2$ 

  ，直径 $d_2$ 

  ）に反力トルク $T_2$ 

を受け，つり合い条件から

$$T_1+T_2 = T \tag{①}$$

 

両端は固定（回転拘束）なので，段付き部の回転角を

$\theta$

とすると

$$\theta = \frac{T_1 l_1}{GJ_1}= -\frac{T_2 l_2}{GJ_2} \tag{②}$$

 

ここで

$$J_1=\frac{\pi d_1^{4}}{32},\qquad J_2=\frac{\pi d_2^{4}}{32}$$

 

2. 反力トルクの比

式 (②) から

$$\frac{T_1}{T_2}= \frac{J_1 l_2}{J_2 l_1} \tag{③}$$

 

3. 反力トルクを決定

(①)(③) を連立すると

$$T_1 = T\;\frac{J_1 l_2}{J_1 l_2 + J_2 l_1},\qquad T_2 = T\;\frac{J_2 l_1}{J_1 l_2 + J_2 l_1}$$

 

4. 段付き部でのねじり角

$$\theta =\frac{T_1 l_1}{GJ_1} =T\frac{J_1 l_2}{J_1 l_2+J_2 l_1}\; \frac{l_1}{GJ_1} =\frac{T\,l_1 l_2}{G\,(J_1 l_2+J_2 l_1)}$$

 

5. 極断面二次モーメントを代入

$$J_1 l_2+J_2 l_1 =\frac{\pi}{32}\left(d_1^{4}l_2+d_2^{4}l_1\right)$$

$$\therefore\; \boxed{\; \theta =\frac{32\,T\,l_1 l_2} {\pi G\bigl(d_1^{4}l_2+d_2^{4}l_1\bigr)} \;}$$

 

---

選択肢との照合

• 分子の係数 → 32
• 分母 →
  $d_1^{4}l_2+d_2^{4}l_1$ 

これは ④ に一致します。

---

答え：④

 

参考：技術士第一次試験－令和2年度機械部門Ⅲ-7解答例 | 技術士のたまご

極断面二次モーメントと断面二次モーメントの違いはなんですか？

断面二次モーメント（ordinary second moment of area）と極断面二次モーメント（polar second moment of area）は、どちらも「断面の形状が力に抵抗する能力」を数値化する指標ですが、力の種類・回転軸の違いによって使い分けます。

---

1. 断面二次モーメント $I$（曲げ剛性指標）

• 定義
  断面をある直線軸（通常は中立軸としての $x$ 軸や $y$ 軸）まわりに曲げたときの抵抗力の度合い。

  $$I_x = \iint_A y^2\,dA,\quad I_y = \iint_A x^2\,dA$$（ここで $x,y$ は断面内の座標、$A$ は断面全体）

• 用途
  梁の曲げ変形解析。曲げモーメント $M$ によるたわみ量 $\delta$ や応力 $\sigma$ の算出に用いる。

  $$\sigma = \frac{M\,y}{I},\quad \delta\propto \frac{M\,L^2}{E\,I}$$

• 単位
  $\mathrm{m}^4$（断面積座標の二乗×面積）

---

2. 極断面二次モーメント $J$（ねじり剛性指標）

• 定義
  断面を中心軸（ねじり軸）まわりにねじったときの抵抗力の度合い。

  $$J = \iint_A \bigl(x^2+y^2\bigr)\,dA = I_x + I_y$$（$I_x, I_y$ は上記の断面二次モーメント）

• 用途
  軸やシャフトのねじり変形解析。ねじりモーメント $T$ による角ひずみ・角変位 $\theta$ の算出に用いる。

  $$\theta = \frac{T\,L}{G\,J},\quad \tau = \frac{T\,r}{J}$$（$\tau$：せん断応力、$r$：断面内の半径方向座標）

• 単位
  こちらも $\mathrm{m}^4$

---

まとめ

指標	計算式	用途
断面二次モーメント $I_x,I_y$	$\displaystyle I_x=\iint y^2\,dA$, $\displaystyle I_y=\iint x^2\,dA$	梁の曲げ剛性
極断面二次モーメント $J$	$\displaystyle J=\iint (x^2+y^2)\,dA=I_x+I_y$	軸のねじり剛性

—断面二次モーメントは「曲げ」、極断面二次モーメントは「ねじり」の剛性を表す、という点が最大の違いです。

極断面二次モーメントになるとｘ軸、ｙ軸それぞれの断面二次モーメントを足したものになるのですか？

はい。極断面二次モーメント $J$ は、断面内の任意点 $(x,y)$ までの距離の二乗で重み付けした面積分

$$J \;=\;\iint_A (x^2 + y^2)\,dA$$

です。一方で

$$I_x = \iint_A y^2\,dA, \quad I_y = \iint_A x^2\,dA$$

なので、

$$\boxed{\,J = I_x + I_y\,}$$

が成り立ちます。つまり極断面二次モーメントは $x$ 軸まわりの断面二次モーメントと $y$ 軸まわりの断面二次モーメントを足し合わせたものです。