 固有角振動数は
$ ω = \sqrt{\frac{ kl^{2} }{J}}$・・・(1)
棒の回転軸周りの慣性モーメントは
$ J = \int_0^l ρr^{2}dr = = \left[ \frac{ρr^{3}}{3} \right]_0^l = \frac{ ρl^{3} }{3} = \frac{ ml^{2} }{3}$
(1)式に代入して、$ ω = \sqrt{\frac{ 3k }{m}}$・・・(1)
[解答]②
参考:
減衰をあらわす係数の意味と求め方
1自由度系の振動 (←このページはボリューミィ読み込めばかなり勉強になる)
固有角振動数は
$ ω = \sqrt{\frac{ kl^{2} }{J}}$・・・(1)
棒の回転軸周りの慣性モーメントは
$ J = \int_0^l ρr^{2}dr = = \left[ \frac{ρr^{3}}{3} \right]_0^l = \frac{ ρl^{3} }{3} = \frac{ ml^{2} }{3}$
(1)式に代入して、$ ω = \sqrt{\frac{ 3k }{m}}$・・・(1)
[解答]②
参考:
減衰をあらわす係数の意味と求め方
1自由度系の振動 (←このページはボリューミィ読み込めばかなり勉強になる)
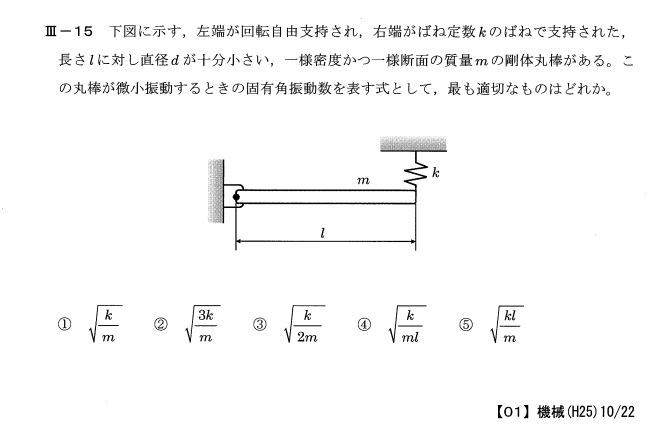
平成25年度技術士第一次試験問題[機械部門] 専門科目Ⅲ-15 回転軸周りの1自由度系の運動方程式
- 更新日:
- 公開日:
 固有角振動数は
$ ω = \sqrt{\frac{ kl^{2} }{J}}$・・・(1)
棒の回転軸周りの慣性モーメントは
$ J = \int_0^l ρr^{2}dr = = \left[ \frac{ρr^{3}}{3} \right]_0^l = \frac{ ρl^{3} }{3} = \frac{ ml^{2} }{3}$
(1)式に代入して、$ ω = \sqrt{\frac{ 3k }{m}}$・・・(1)
[解答]②
参考:
減衰をあらわす係数の意味と求め方
1自由度系の振動 (←このページはボリューミィ読み込めばかなり勉強になる)
固有角振動数は
$ ω = \sqrt{\frac{ kl^{2} }{J}}$・・・(1)
棒の回転軸周りの慣性モーメントは
$ J = \int_0^l ρr^{2}dr = = \left[ \frac{ρr^{3}}{3} \right]_0^l = \frac{ ρl^{3} }{3} = \frac{ ml^{2} }{3}$
(1)式に代入して、$ ω = \sqrt{\frac{ 3k }{m}}$・・・(1)
[解答]②
参考:
減衰をあらわす係数の意味と求め方
1自由度系の振動 (←このページはボリューミィ読み込めばかなり勉強になる)