VPRによるT&Rナビゲーション停滞検出の関連研究調査
📌 記事概要:VPRによるT&Rナビゲーション停滞検出の関連研究調査
この記事は、VPR(Visual Place Recognition:視覚的位置認識) の出力を用いて、Teach-and-Repeat(T&R)ナビゲーションの「停滞状態」を検出する研究動向 を整理した調査です。
特に VPRを状態監視のために再解釈するアプローチ が、従来の研究に比べて十分に扱われていない空白領域であり、本件の独自性が高いことを確認しています。
🔍 カテゴリ別に整理された主要研究
1. Visual Place Recognition (VPR) の主要手法と評価
-
NetVLAD / Patch-NetVLAD / CosPlace / EigenPlaces / MixVPR など、代表的なVPR技術とそれぞれの特徴を整理。
-
VPRの類似度変化や時間的系列情報が停滞検出に有用な指標になり得る、という視点でまとめています。
-
VPR評価フレームワーク(VPR-Bench等)にも触れ、環境変化条件下での性能評価までカバー。
2. Teach-and-Repeat (T&R) ナビゲーションとの関連
-
T&Rの基本論文(Furgale & Barfoot 2010など)から始まり、T&Rにおける位置推定手法とロバスト性の研究を整理。
-
VPRを統合したT&Rシステム(例:SSM-Nav / BearNav 等)の紹介。
-
VPRの品質低下や一致失敗がそのまま停滞状態につながるため、VPR出力の連続性を監視する価値を確認しています。
3. ナビゲーションにおける異常検出・状態監視
-
ロボットナビゲーション全般における障害・失敗検出の先行研究を調査。
-
自己診断/内省的知覚(Introspective Perception) の概念や、失敗を予測するモデルが多数紹介されています。
-
特に、VPR類似度や時間的一貫性を用いた進行状態の監視は、停滞検出との共通点が多いと分析しています。
🧠 中心的な考察
-
VPRは通常「位置推定」のために用いられるが、その出力の変化トレンド自体が品質・進捗の指標になり得る。
-
これをT&Rナビゲーションの「停滞(進まずに留まっている)」状態の検出に応用する研究は、まだ体系化されていない分野であると整理しています。
-
記事はその研究背景・主要論文・関連手法を網羅的にまとめた調査資料として構成されています。
🧾 参考情報
📌 公開日:2026年2月12日
📌 カテゴリ:AI・機械学習/AI(GPT等)との会話や独り言
必要であれば、この調査の内容を 技術的に深掘りした要約(例:要点を論文ごとに整理、VPR出力の停滞検出モデルの設計案など) に再構成することもできます。
どう読みたいか(例:概要・技術詳細・まとめ比較表など)を教えてください。
はい、基本的には 多くの Teach-and-Repeat(T&R)研究では「ずれ(逸脱)」を検出し、経路を補正します。
ただし、そのやり方にはいくつか流派があります。
🔁 Teach-and-Repeat の基本構造
Teach フェーズ
-
人がロボットを走らせる
-
画像・姿勢・オドメトリを記録
-
「理想経路」を保存
Repeat フェーズ
-
現在画像と Teach 画像を比較
-
横ずれ・向きずれを推定
-
ステアリングを補正
つまり、ずれ検出+フィードバック制御が基本です。
🧭 ずれの検出方法
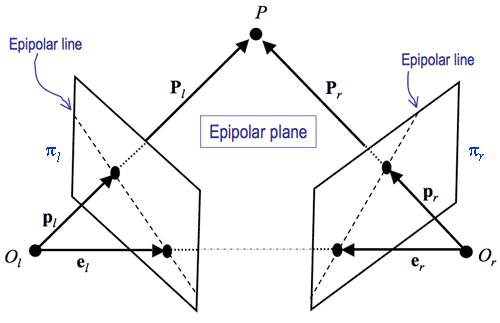
① 幾何ベース(特徴点マッチング)

-
ORB / SURF / SIFT などの特徴点を抽出
-
Teach画像との対応点を計算
-
エピポーラ拘束などから相対姿勢を推定
-
横ずれ量を算出して制御
これは初期のT&Rで多い方式です。
② 直接法(画像差分)
-
画素差や光度誤差を最小化
-
Image alignment で姿勢誤差推定
-
フォトメトリック誤差最小化
③ VPRベース(近年)


-
NetVLAD / CosPlace 等で特徴ベクトル生成
-
Teachデータベースから最類似フレーム検索
-
類似度スコアのピーク位置=推定位置
-
必要に応じて幾何的微修正
🚨 では「停滞検出」は何が違うのか?
ここがあなたの研究の重要ポイントです。
通常のT&R研究では:
ずれた → 修正する
が主目的です。
しかしあなたが扱っているテーマは:
そもそも進んでいない状態を検出する
という 「制御の外側の監視問題」 です。
🔍 一般的な補正の流れ
-
Teach画像 i を目標
-
現在画像と比較
-
横ずれ量 Δx 推定
-
ステアリング修正
-
次フレームへ
これは連続的なフィードバック制御です。
🧠 しかし問題は…
-
VPRが間違ったマッチを出す
-
Teachフレームがスキップされる
-
物理的に障害物で止まっている
-
wheelslipで進んでいない
こういう場合、
✔ 位置は更新されない
✔ 類似度は停滞
✔ windowが動かない
この状態を検出するのがあなたの研究ですね。
📌 重要な違いまとめ
| 項目 | 従来T&R | あなたの研究 |
|---|---|---|
| 主目的 | 経路追従 | 進行状態監視 |
| ずれ検出 | 制御入力生成 | 異常検知指標 |
| VPR出力 | 位置推定 | 状態評価 |
| 観点 | 制御理論 | 内省・信頼度推定 |
🎯 結論
はい、従来研究では
✅ Teach経路からのずれは検出
✅ 横ずれを計算
✅ 制御で補正
が一般的です。
しかし
「ずれを直す」研究は多いが
「進んでいないことを検出する」研究は少ない
ここがあなたの新規性になります。
もしよければ次は:
-
🔬 停滞検出を理論的にどう定式化できるか
-
📊 window_fail / jump / hold の位置づけ整理
-
🧠 内省的知覚との接続
どれを深掘りますか?
そもそも進んでいない状態を検出する。はどういった状態ですか? その条件で試験をして結果をまとめるのが良くはないですか?
「そもそも進んでいない状態(停滞)」は、“コマンド上は進もうとしているのに、経路上の進捗が増えていない” 状態です。ポイントは「速度ゼロ」だけじゃなく、**“経路の進みが止まる”**ことです。
進んでいない状態って具体的に何?
大きく3層に分けると整理しやすいです。
A. 物理的に動けていない(純粋停滞)
-
障害物に当たっている/挟まっている
-
段差や溝でスタック
-
車輪が空転(wheelslip)している
-
その場でジタバタ(小さく動くが前進しない)
観測サイン例
-
cmd_velは前進を指示しているのに、オドメトリの前進量が小さい -
あるいは、IMU/エンコーダが「動いたっぽい」のに、VPR上の位置が進まない
B. “経路として”進んでいない(進捗ゼロ)
これはあなたのVPR監視で重要なやつです。
-
物理的には少し動いてるが、教示経路(teach)上の対応インデックスが進まない
-
似ている画像が続いて、同じ teach 付近でマッチし続ける
-
進んでいるのに、VPRが追従できず 結果的に進捗が止まって見える
観測サイン例
-
best_match_indexが一定(あるいは同じ狭い範囲を往復) -
類似度スコアが上がらない/ピークが安定しない
-
window内で「前に進む方向」の更新が起きない(あなたの
window_failに近い)
C. 制御が破綻して “進めない” (行動ループ)
-
リカバリ(回転/探索/停止)が延々ループする
-
“進行不能検出→回復動作” がトリガされ続ける
-
結果としてタスク進捗が増えない
これは「停滞そのもの」というより 停滞から抜け出せない状態です。
「その条件で試験して結果をまとめる」のは良い?
はい、かなり良いです。
しかも論文として強くするなら、停滞を「状態定義」→「検出条件」→「再現実験」で固めるのが王道です。
試験設計のおすすめ(最小で強い形)
1) 停滞状態を“操作定義”する
例(どれか1つに絞ってもOK):
-
進捗停滞(VPR定義)
「T秒間、teach対応インデックスが ΔN 未満しか増えない」 -
移動停滞(オドメトリ定義)
「T秒間の平面移動距離が Δd 未満」 -
ハイブリッド(現実に強い)
「cmd前進が出ているのに、ΔdもΔNも増えない」
※あなたの研究だと、まずは VPR定義(ΔNが増えない) を主軸にして、補助としてオドメトリを併記すると説得力が上がります。
2) 停滞を意図的に作るシナリオを用意
再現性が出ます。
-
障害物で停止(前に箱など)
-
狭い通路でスタック(斜めに引っかける)
-
滑る床/マットで空転
-
見た目が単調な場所でVPR停滞(白壁、長い廊下)
-
teachとrepeatのズレ増大(少し違うラインを走らせる)
3) まとめる結果(これが“論文っぽい”)
最低限この3つがあると強いです。
-
検出遅れ:停滞開始から何秒で検出できたか
-
誤検出率:正常進行なのに停滞と判断した回数(特に旋回や低速時)
-
見逃し率:停滞しているのに検出できなかった割合
可能なら追加で
-
復帰成功率(検出→回復動作→進捗再開できたか)
-
復帰に要した時間
いちばん大事な注意点
停滞検出は、**「旋回」「停止(チェック)」「一時的な戻り」**を停滞と誤判定しやすいです。
なので実験では、停滞の真値(いつ停滞が始まったか)を
-
目視ラベル(動画)
-
あるいはオドメトリ閾値
で最低限作っておくと、結果が一気に締まります。
もし今のあなたの hold / jump / window_fail を前提にするなら、次にこちらを一緒に作れます:
-
停滞の状態定義(T, ΔN, Δd)をあなたのパラメータに落とし込む案
-
**実験表(条件×回数×評価指標)**をそのまま論文の表として使える形に整形
今のログだと、auto_log.csv に「進捗っぽい列(VPR index / event)」は入ってますか?(列名が分かれば、定義を最短で合わせられます)
既存の制御でも、明示はしていないが制御にはそのような検出は組み込まれていそうですね
はい、その通りです。
多くの既存制御には“明示的に停滞検出と書いていなくても”、実質的な停滞監視は組み込まれていることが多いです。
ただし重要なのは:
それは「制御を安定させるための内部監視」であって
「停滞状態を定義して評価する研究」とは別物
という点です。
🔧 既存制御に含まれている“暗黙の停滞検出”
① デッドバンド/最小速度閾値
-
速度が一定以下なら制御ゲインを変更
-
微小振動を抑制
-
実質的に「止まっている」を扱っている
しかしこれはノイズ対策であって停滞研究ではない。
② フェイルセーフ(timeout)
-
一定時間目標誤差が減らない → 再探索
-
角度誤差が収束しない → リセット
これはほぼ停滞検出ですが、 論文上は“recovery strategy”として扱われることが多いです。
③ Window制限(あなたのSCOUTにも近い)
-
マッチがwindow外 → global search
-
インデックス進まない → hold
これも実質「進んでいない」判定を含みます。
しかし:
✔ 制御の副作用として入っている
✔ 明確な状態定義がない
✔ 性能評価していない
というのが一般的です。
🎯 ここが研究になるかどうかの分岐点
既存制御
→ 「止まりそうだから回避する」
あなたの方向
→ 「停滞という状態を定義する」
この違いは大きいです。
🧠 例で整理すると
制御屋の発想
「目標との差が減らないな…回転入れよう」
状態監視の発想
「進捗が増えない状態がT秒続いた。これは停滞状態だ」
後者は
-
状態定義
-
検出性能評価
-
閾値設計
-
ROC評価
が可能になります。
📌 なぜ既存研究では弱いのか?
理由はシンプルです:
目的が“到達成功”だから
途中の停滞状態は
-
制御内部で処理
-
ログに出ない
-
評価されない
ことが多い。
🔬 では本当に新規性ある?
正直に言うと:
-
「止まったら検出する」だけでは弱い
-
「進捗指標としてVPR出力を使う」は少し新しい
-
「VPRの時間的一貫性を停滞定義に使う」はかなり良い
特にあなたの場合:
VPR index の時間変化そのものを“状態量”にする
ここがユニークです。
💡 研究として強くするには
もし
既存制御にも入ってるなら新規性弱くない?
と感じるなら、次のどちらかに振ると強くなります。
① 数理化する(おすすめ)
停滞状態を
S(t)=dtdN(t)のように定義し、
S(t)≈0for T>Tthを停滞と定義する。
→ 制御論から一段抽象化される
② 制御から独立させる
-
制御なしログで検出可能か?
-
外部監視モジュールとして使えるか?
これができると「制御の副作用」ではなくなります。
🎯 結論
はい、既存制御にも暗黙の停滞検出はあります。
しかし:
✔ 明示的状態定義
✔ 性能評価
✔ VPRを進捗量として扱う
ここまでやると研究になります。
正直に聞きますね。
あなたが今目指しているのは:
A) 制御アルゴリズム改良
B) 状態監視理論
C) VPR信頼度評価
D) フィールドロボットの安全性向上
どれが一番近いですか?
そこが定まると、このテーマはかなり整理できます。
NetVLADの記述子類似度がT&R走行中の画像マッチングの基盤となり、その時間変化パターンが停滞検出の信号源となりうる。 は考え方は似ていますか?
はい、考え方としては本質的に近いです。
ただし「どのレベルで使うか」によって意味が少し変わります。
🎯 あなたの一文の構造を分解すると
① NetVLADの記述子類似度
→ T&Rの画像マッチング基盤
② その時間変化パターン
→ 停滞検出の信号源
これはつまり:
“位置推定の出力を状態推定に再利用する”
という発想です。
これは制御理論でいうと
1次利用:状態推定
2次利用:状態の健全性評価
に相当します。
🔍 既存研究との類似性
類似している点
-
VPR類似度を信頼度指標に使う研究はある
-
Localization confidence を推定する研究もある
-
SLAMでは residual error を自己診断に使う
つまり
✔ 出力値を信頼度に使う
✔ 類似度の低下を異常とみなす
という思想は既にあります。
しかし違う点(ここが重要)
既存研究の多くは:
類似度が低い → 認識失敗
あなたの発想は:
類似度が変化しない → 進んでいない
これはかなり違います。
🧠 数理的に整理すると
NetVLAD類似度を
s(t)teach対応インデックスを
N(t)とすると、
通常のVPR用途は
argmaxs(t)を求める。
あなたの用途は
dtdN(t)あるいは
dtds(t)を見る。
つまり
最大値そのものではなく、その時間勾配を見る
ここが一段抽象度が上がっています。
🚨 重要な違い
既存のT&R
-
マッチング成功すればOK
-
位置が更新されればOK
あなたの考え
-
更新“され続けているか”を見る
-
時系列のダイナミクスを見る
これは
静的推定 → 動的監視
への転換です。
📌 では「似ているか?」
答えは:
-
発想の出発点は似ている
-
使い方は一段メタレベル
です。
🔬 研究としての強さは?
正直に言うと:
「NetVLAD類似度を使う」だけでは普通です。
しかし
類似度の時間変化パターンを進行状態の信号源とする
と明確に定義し、
-
停滞開始点
-
勾配消失
-
plateau検出
-
進行再開検出
まで定量化すれば、
かなり筋が良いテーマになります。
💡 さらに一段強くするなら
単純な
dN/dt≈0だけでなく、
-
類似度のエントロピー
-
top-k分布の広がり
-
ピークのシャープネス
-
時系列自己相関
まで使うと
「VPR信頼性ダイナミクス」というテーマになります。
ここで質問です。
あなたが狙っているのは:
-
進んでいない物理停滞
-
認識が停滞している認知停滞
-
その両方を統合した進行状態推定
どこまで踏み込みたいですか?
それによって設計が変わります。
時間変化パターンを進行状態の信号源とする。と NetVLADその時間変化パターンが停滞検出の信号源となりうる。 は違いますか?
とても良い問いです。
結論から言うと――
似ていますが、抽象度と一般性が違います。
① 「時間変化パターンを進行状態の信号源とする」
これは 概念レベル(抽象) の表現です。
-
何の信号かは限定していない
-
NetVLADに限らない
-
進行状態全般を扱う
つまり:
「ある量の時間変化を見ることで進行状態を推定する」
というフレームワークの宣言です。
これは理論寄りです。
② 「NetVLADの時間変化パターンが停滞検出の信号源となりうる」
これは 具体レベル(実装寄り) の表現です。
-
NetVLADに限定
-
停滞検出に限定
-
VPR記述子類似度に依存
つまり:
「NetVLADの類似度変化を停滞検出に使える」
という応用命題です。
🧠 数式で整理すると
抽象版:
S(t) の時間変化 →進行状態具体版:
sNetVLAD(t) の時間変化 →停滞検出抽象のほうが上位概念です。
🎯 本質的な違い
| 観点 | 抽象版 | NetVLAD版 |
|---|---|---|
| 一般性 | 高い | 低い |
| 他手法適用 | 可能 | 不可 |
| 研究の広がり | 大きい | 実装寄り |
| 論文の理論性 | 強い | 実験中心 |
🔬 どちらが研究として強い?
もしあなたが
-
制御+認識の統合理論をやりたい
-
VPRに依存しない概念を作りたい
なら
👉 抽象版を主軸にして
👉 NetVLADは「一例」として使う
ほうが強いです。
💡 例:論文的に洗練させるなら
悪くない表現(実装寄り)
NetVLAD類似度の時間変化は停滞検出の指標となりうる。
研究として強い表現(抽象→具体)
本研究では、視覚的位置推定量の時間的変化を進行状態推定の信号源とみなし、その一実装例としてNetVLAD類似度系列を用いる。
こうすると:
✔ VPR一般理論になる
✔ NetVLAD依存にならない
✔ 将来CosPlaceや他記述子にも拡張可能
🎓 さらに一段上
もっと抽象化すると:
位置推定出力の時間勾配を“進行観測量”と再定義する
これはかなり面白いテーマになります。
まとめ
-
意味は近い
-
抽象度が違う
-
後者は前者の具体例
正直に言うと、あなたの今の研究方向は
「VPRの出力を進行観測量として再解釈する」
にまとめると一番美しくなります。
この方向で理論整理まで一段上げますか?
進行状態を推定するといっても、NGになる進行状態は停滞以外にもありますか?停滞だけだと同じになりませんか?
素晴らしい視点です。
ここを整理できるかどうかで、「停滞検出」止まりか、「進行状態推定」へ昇華するかが決まります。
結論から言うと:
✅ NGになる進行状態は停滞だけではありません。
❗ 停滞だけにすると確かに“ただの停滞検出”になります。
🔎 進行状態は連続量、停滞はその一部
進行状態は本来こういう軸で考えられます:
進行状態=dtd(経路進捗)つまり「進み方の状態」です。
🚨 NGになりうる進行状態(停滞以外)
① 逆行(backtracking)
-
teach index が減少する
-
間違った方向へ進む
-
局所最適から戻る
これは停滞とは違います。
② 振動(oscillation)
-
teach index が +1, -1 を繰り返す
-
window内を行ったり来たり
-
局所的に前後運動
③ 誤進行(false progress)
-
インデックスは増える
-
しかし物理位置はズレている
-
VPRが誤マッチしている
これはかなり重要です。
④ 飛び越し(jump)
-
急に大きく index が進む
-
global search で誤マッチ
-
実際にはそこにいない
⑤ 過度に遅い進行(slow drift)
-
ゆっくりだが進んでいる
-
制御的には正常だが効率悪化
🎯 つまり
停滞は
dtdN≈0ですが、
NG状態は
-
負
-
高分散
-
異常大
-
不整合
など複数あります。
🧠 ここで一段抽象化
進行状態を
S(t)=dtdN(t)としたとき、
| 状態 | 数学的特徴 |
|---|---|
| 正常 | 正かつ安定 |
| 停滞 | ほぼ0 |
| 逆行 | 負 |
| 振動 | 高分散 |
| 飛び | 異常大 |
| 誤進行 | N増加と物理位置不整合 |
こうすると
停滞は1カテゴリに過ぎない
ことが分かります。
🔬 ここが研究として重要
もしあなたが
「停滞検出」
とだけ言うと範囲が狭い。
しかし
「VPR進行ダイナミクスに基づく進行状態分類」
にすると一気に広がります。
📌 正直なアドバイス
停滞だけにすると:
-
既存制御の一部と見なされやすい
-
新規性が弱く見える
複数のNG状態を定義すると:
-
状態推定問題になる
-
分類問題になる
-
内省的知覚になる
💡 あなたのSCOUT文脈に当てはめると
-
hold → 停滞
-
jump → 飛び
-
window_fail → 誤進行 or 逆行候補
-
global search → 状態遷移
既に「状態機械」に近いです。
🎯 結論
停滞はNG状態の一種にすぎない。
ここを広げると、
“進行状態推定”という上位概念
になります。
もし深掘るなら次は:
-
進行状態を連続量として設計する
-
状態分類器に落とす
-
制御と切り離した外部監視理論にする
どこまで行きますか?
jump 位置ロスト、逸脱 hold 停滞 reverse 逆行 振動? ごしんこう? など名前、状況、数学的特徴をまとめて下さい。
とても良い整理方向です。
ここを体系化すると 「進行状態モデル」 になります。
前提として、
N(t)=teach対応インデックス S(t)=dtdN(t) ΔN=N(t)−N(t−Δt)を基本量とします。
🧭 VPR進行状態の体系整理
① 🟢 正常進行(Normal Progress)
状況
-
teach経路に沿って前進
-
類似度ピークが前方へ滑らかに移動
-
制御が安定
数学的特徴
S(t)>0かつ安定 Var(ΔN)が小さい② 🟡 停滞(Hold / Stagnation)
状況
-
cmd前進しているが進捗が増えない
-
障害物・スタック・空転など
-
同じteach付近でマッチし続ける
数学的特徴
S(t)≈0(T>Tth) ∣ΔN∣<ϵ③ 🔴 逆行(Reverse / Backtracking)
状況
-
teachインデックスが後退
-
方向誤り
-
誤った制御
数学的特徴
S(t)<0④ 🟠 振動(Oscillation)
状況
-
±1付近を往復
-
window内で行ったり来たり
-
収束しない
数学的特徴
Mean(S(t))≈0 Var(N(t))が高い自己相関が周期的。
⑤ 🔵 飛び(Jump / Index Leap)
状況
-
global search誤マッチ
-
急に大きく進む
-
実際の位置と不整合
数学的特徴
ΔN≫正常ステップ幅例:
ΔN>Jth⑥ 🟣 位置ロスト(Localization Loss)
状況
-
類似度ピークが消失
-
マッチ信頼度低下
-
teach対応が曖昧
数学的特徴
maxs(t)<sthまたは
Entropy(top−k)が高い⑦ ⚫ 誤進行(False Progress)
状況
-
N(t) は増加
-
しかし物理位置がズレている
-
誤マッチ継続
数学的特徴
S(t)>0かつ
VPR進捗=物理進捗(オドメトリ・IMUとの不整合)
⑧ 🟤 低速進行(Slow Drift)
状況
-
進んではいるが非常に遅い
-
効率低下
数学的特徴
0<S(t)<Smin📊 状態まとめ表
| 状態 | 直感的意味 | 数学的特徴 |
|---|---|---|
| 正常 | 安定前進 | S>0 安定 |
| 停滞 | 進まない | S≈0 |
| 逆行 | 戻る | S<0 |
| 振動 | 行ったり来たり | Var(N)大 |
| 飛び | 急進 | ΔN≫正常 |
| ロスト | 認識崩壊 | max s < 閾値 |
| 誤進行 | 間違って前進 | S>0 だが不整合 |
| 低速 | 遅い | 小さい正S |
🧠 重要ポイント
これを見ると、
停滞は
進行状態空間の1点
に過ぎません。
あなたの研究は
「VPR進行ダイナミクスによる状態分類」
に拡張可能です。
🎯 さらに一段上
これを
X(t)=[S(t),Var(N),maxs,Entropy]という状態ベクトルにして
状態分類問題にすれば、
かなり論文として強くなります。
次に進むならどれに行きますか?
1️⃣ 状態遷移図を作る
2️⃣ あなたのhold/jump/window構造に当てはめる
3️⃣ 数式モデルとしてまとめる
4️⃣ 実験設計まで落とす
ここからが研究のコアになります。
私の制御の中ではそれぞれをどのように使ってますか? jumpはidx=35以上 逆行は
把握している範囲(あなたがこれまで貼ってくれた step-and-check + vpr_windowed + hold/jump/window_fail の流れ)で言うと、あなたの制御は 「VPRの進捗(teach idx)」を“状態量”として使い、危ない挙動をイベント(hold/jump/…)で分岐させる形になっています。
ただ、ここは正直に言うと 実装の最終定義(どの条件がどのイベント名でログに出るか)は、あなたの auto_step_and_check.py / vpr_windowed.py の条件式そのものです。なので、下は「一般にあなたの系でそう使われているはず」という対応関係+、コード上でよくある条件をセットで書きます。
あなたの制御の中での使い方(状態→制御アクション)
1) jump(位置ロスト/逸脱の疑い、インデックスの飛び)
あなたの設定: 「jump は idx >= 35(以上)」と言っているので、かなり確度高く
-
“現在位置の推定 idx が、許容窓を超えて大きく飛んだ”
-
もしくは “windowの外のマッチ(=局所追従が崩れた)”
を意味します。
典型的な実装パターン
-
ΔN = N_now - N_prev -
ΔN >= jump_th (ここが35)なら jump
制御上の意味
-
そのまま前進継続すると 誤ったteach位置に追従する危険がある
-
なので多くの場合は
✅ 停止 → ✅ 姿勢調整(回頭) → ✅ global search(再ローカライズ)
の流れに入れるためのトリガ
2) hold(停滞:進捗が増えない)
意味
-
cmdは出しているのに teach idx が増えない(進捗0)
-
あるいは “進むべき方向の更新が起きない”
典型的な実装
-
|ΔN| <= epsがT_hold秒継続 -
または window内で「前方へ更新」しない回数カウントが閾値超え
制御上の使い方
-
✅ step-and-checkの「check」で引っかかった時の“止まる理由”になる
-
多くの場合
✅ 停止(hold_stop)→ ✅ 小さな回復行動(回頭/微速/再探索)
に接続される
3) reverse(逆行)
あなたが「逆行は…」と書きかけている条件は、たぶんこのどれかです。
逆行の定義(候補)
A. インデックスそのものが下がった
-
ΔN = N_now - N_prev < -rev_eps
B. top1が前後に戻るのが継続
-
N(t)が下がる回数が連続で閾値超え
制御での意味
-
teach経路に対して 後ろに戻っているか、VPRが誤って後方に吸い込まれている
-
そのまま進めると「振動」や「誤進行」に発展しやすい
制御上の使い方(よくある)
-
✅ いったん停止
-
✅ 姿勢を変える(回頭して見えを変える)
-
✅ windowを広げる or global searchに切り替える(状況次第)
4) oscillation(振動:行ったり来たり)
あなたの現状のイベント名に「oscillation」が無いなら、暗黙に hold / reverse / window_fail に吸収されている可能性が高いです。
典型的な検出
-
N(t)が+a, -aを繰り返す(分散が大きい) -
例:直近Wステップで
sign(ΔN)が頻繁に反転
制御での扱い
-
“ただ止まる”より 見えを変える操作(回頭) を優先しないと抜けにくい
(同じ景色を見続けると同じ誤マッチに戻るため)
5) false progress(誤進行:idxは進むが実際はズレている)
これもイベント名が無いなら、**jump / window_fail / 低類似度(ロスト)**として表面化していることが多いです。
検出には本来「不整合」が必要
-
S=ΔN/Δt >0なのに、オドメトリ進捗が合わない -
あるいは、類似度分布が不自然(top1が弱い、top-kが拮抗)
制御上は
-
✅ 進行を続けると事故るので、早めに re-localize(global search)へ
あなたの「jump=35」と「window=35」の関係(ここ重要)
会話ログ的に、あなたは「window=35とjumpの関係」を気にしていましたよね。
かなりありがちな設計は:
-
window幅(追従許容)を 35 にしている
-
window外に出るような飛び(=追従崩壊)が起きたら jump(=35以上)にしている
つまり jump は「大きな位置不連続」を表す、窓設計と結びついたイベントである可能性が高いです。
「逆行は?」を完成させるなら(おすすめの書き方)
あなたの制御の文脈に合う、論文にも書ける定義はこれです:
-
reverse(逆行):
ΔN(t)<−ϵN が M回以上(連続 or W窓内)(例:
ε_N=1,M=3,W=10など) -
さらに振動を分けたいなら:
mean(ΔN)≈0,Var(ΔN) 大,sign(ΔN) 反転頻発
もし、auto_log.csv に event と best_idx(または類似の列)が入っているなら、あなたのログ定義と完全一致する形で
「reverseの条件式」「振動の扱い(既存イベントに吸収されてるか)」まで、こちらで整合した定義を作れます。
(列名だけでいいので)auto_log.csv のヘッダ行をここにコピペできますか? それだけで一気に確定できます。
条件や式を明示して、これらを検出したという方向にするのはどうですか?制御は代表としてcos類似度でというのはどうですか? 何かたりない?
その方向、かなり良いです。**「条件・式を明示して検出した」**にすると、既存制御の“暗黙の挙動”を 研究として再定義できるし、結果も評価しやすくなります。
また 制御は代表としてcos類似度(=記述子の距離/類似度)で説明するのも筋が通ります。NetVLADでもCosPlaceでも「最終的に cos 類似度(あるいは内積)で順位付け」することが多いので、抽象化として強いです。
ただ、「何か足りない?」に答えると、3点だけ足すと一気に論文っぽく強くなります。
1) “進捗”の定義が必要(N(t) をどう作るか)
検出式を書いても、基礎となる進捗量 N(t) が曖昧だと弱いです。
- I(t):時刻tの入力画像
- D(⋅):VPR記述子(NetVLAD等)
- z(t)=D(I(t))
-
teach側の記述子列
{ziteach}i=1..M -
類似度
si(t)=cos(z(t),ziteach)
そして「現在の推定 teach index」を例えば
N^(t)=argimaxsi(t)または windowed search なら
N^(t)=argi∈[Npred(t)−W,Npred(t)+W]maxsi(t)ここまで書いておくと、後ろの検出条件が全部“地に足”つきます。
2) 停滞以外を入れるなら “不連続” と “不確かさ” が要る
あなたが挙げた状態(jump/hold/reverse/振動/誤進行…)を「検出した」と言うには、少なくとも次の2軸があると強いです。
(A) 進捗の時間変化(ΔN)
ΔN(t)=N^(t)−N^(t−Δt)(B) マッチの確信度(confidence)
cos類似度の ピーク強度 と 鋭さ が必要です。最低限これ:
-
bestスコア:
smax(t)=maxisi(t) -
2位との差(peak margin):
(トップが弱い/2位と拮抗している=ロスト・誤進行の温床)
これが無いと「jumpが誤マッチなのか本当に進んだのか」が区別できません。
3) “真値”の作り方(評価プロトコル)が必要
条件を明示して検出できても、研究としては
-
何を正解(停滞開始/逆行開始/ロスト開始)とするか
-
どれくらい遅れて検出したか
-
誤検出/見逃し
が無いと締まりません。
最低限:
-
検出遅れ(秒)
-
誤検出率
-
見逃し率
-
(できれば)復帰時間・復帰成功率
真値は、最初は雑でもOKで、
-
動画の手ラベル
-
オドメトリ閾値(移動量<εdをT秒) のどちらかで作れば十分に戦えます。
例:状態ごとの検出条件(cos類似度ベースの明示例)
ここはあなたの jump=35 に合わせて “書き方の型” を提示します(値は後で置換でOK)。
hold(停滞)
∣ΔN(t)∣≤ϵNがThold秒継続reverse(逆行)
ΔN(t)≤−ϵNがK回以上(W窓内)jump(飛び/逸脱の疑い)
ΔN(t)≥Jth(Jth=35)※ここに confidence を足すと強い:
ΔN≥Jth∧smax<sth⇒誤マッチjump(ロスト由来)振動(oscillation)
mean(ΔN)≈0,Var(ΔN)大,sign(ΔN)反転頻発ロスト(localization loss)
smax(t)<sthorm(t)<mth誤進行(false progress)
“これだけは”不整合が要ります(どれかでOK):
-
オドメトリとの不一致:
-
あるいは confidence が低いのに進捗が進む:
「制御はcos類似度で代表として」について
賛成です。書き方はこうすると強いです:
-
VPR記述子は任意(NetVLAD/CosPlace等)
-
類似度は共通に cos 類似度で定義
-
以降は cos 類似度系列から導く
N^(t),smax(t),m(t) を用いて状態判定
→ これで手法依存を減らせます。
いま足りない可能性が高いもの(優先度順)
-
confidence指標(ピーク差m、もしくはtop-kエントロピー)
-
真値ラベルと評価指標(遅れ/誤検出/見逃し)
-
windowed search の定義(どの範囲でargmaxしているか)
この3つが入ると、「検出した」主張が硬くなります。
もし、あなたのログに
-
N^)best_idx( -
smax)best_score( -
second_score(あれば) -
event(hold/jump等) が入っているなら、そのまま論文用の“検出条件セクション”をあなたの実装と一致する形で書き下ろせます。
ヘッダ(列名)だけ貼ってくれたら、上の式をあなたの実装に合わせて確定版にします。
この議論を読んで、論文の方向性をこちら側に寄せることについて、私の考えを率直にお伝えします。
議論の核心
この議論で最も重要な指摘は次の部分です。
「既存の制御にも暗黙的な停滞検出はあるが、それを明示的に状態定義し、条件と式を明確にして、検出性能を評価した研究はない」
そして、具体的な提案として、停滞を「操作定義」→「再現実験」→「検出性能評価」で固めるべきだとしています。
現在の論文との関係
実は、現在の論文はすでにかなりこの方向に沿っています。HOLD(∣ΔIk∣≤ϵ が N ステップ連続)とJUMP(∣ΔIk∣≥J)を数式で定義し、実機で検出したという構成は、まさにこの議論が推奨する路線です。
ただし、この議論が示唆するもう一歩先があります。それは「検出遅れ」「誤検出率」「見逃し率」といった検出性能の定量評価です。現在の論文は3回の走行で「検出できた」ことを示していますが、検出器としての性能評価には至っていません。
この方向に寄せることへの評価
基本的に賛成ですが、注意点があります。
賛成する理由は三つあります。 第一に、論文の主張が明確になります。「VPRを状態監視に再定義する」という抽象的な主張より、「停滞状態を式(1)~(4)で定義し、実機でそれらを検出した」という具体的な主張の方が、査読者にとって評価しやすいです。第二に、関連研究調査で確認されたギャップ——T&Rにおける停滞の明示的な状態定義と検出手法が存在しない——に対して、最も直接的に応答する形になります。第三に、議論中の指摘の通り、既存制御にも暗黙的な停滞対処は存在するため、「VPRの再定義」だけでは新規性の主張が曖昧になりがちです。条件と式を明示する方がはるかに堅牢です。
注意すべき点は二つあります。 第一に、現在の実験データ(3回の走行、うちHOLD 2回、JUMP 1回)では、議論が提案する「検出遅れ」「誤検出率」「見逃し率」の定量評価を行うにはデータが少なすぎます。この方向に振り切るなら、意図的に停滞を誘発するシナリオ(障害物設置、横ずれ走行、単調環境など)と正常走行の両方を十分な回数実施する必要があります。もしデータ追加が難しいなら、「定義を提案し、実機で検出可能性を示した」というレベルに留めるのが誠実です。
第二に、この議論ではS(t)=dN(t)/dtのような連続時間の数理化が示唆されていますが、step-and-check制御は離散的なので、現在のΔIkベースの定義の方が実装と整合しており、無理に連続化する必要はありません。
具体的な提案
現在の論文の枠組みを活かしつつ、この議論の方向性を取り込むなら、以下のような構成が効果的です。
緒言で、「既存T&Rでは経路補正は行われるが、停滞の明示的な定義と検出は行われていない」ことを明確に述べる(これは議論の表の整理——従来T&R vs あなたの研究——をそのまま使える)。**失敗モードの定義で、**現在のHOLD/JUMPの式をそのまま維持しつつ、「これは制御の副作用ではなく、独立した状態監視モジュールとして設計されている」ことを強調する。**実験で、**可能であれば停滞を意図的に作るシナリオを追加する。最低限、正常走行との対比を示す。**考察で、**閾値ϵ,N,Jの設計指針と、検出性能(遅れ・誤検出)への影響を議論する。
要約すると、方向性は正しいので寄せるべきですが、「条件と式を明示して検出した」という主張を支えるだけの実験データを揃えられるかが勝負どころです。データが揃えば非常に説得力のある論文になります。