了解です。
これは Fusion の仕様問題なので、あなたの操作や理解の問題ではありません。
他の人（同僚・フォーラム・サポート）に相談できるように、
現状・詰まっている点・結論・回避策を整理した「そのまま貼れるまとめ」を作ります。

---

Fusion でヘルツ接触解析を行った際の現状整理（共有用）

1. やりたいこと（目的）

• 球（半球）と平板の ヘルツ接触解析を Fusion Simulation で実施
• 結果として得られた 接触圧力分布から
  接触半径（接触円の半径）を測定し、理論解と比較したい

---

2. 解析設定の状況（ここまでは問題なし）

• 解析タイプ：静解析（Static Stress）
• 接触：
  • Frictionless
  • Bonded ではない
• 平板：固定拘束（剛体扱い）
• 球：分布荷重を付与
• メッシュ：
  • 接触部に局所メッシュ（十分に細かい）
• 結果表示：
  • 「接触圧力（合計）」を表示
  • 断面（Section）を入れて接触領域を線として可視化

👉 接触圧力分布自体は正しく出ている
👉 円形の接触領域も確認できている

---

3. 問題点（詰まっているところ）

問題①

Simulation の結果表示画面では「距離測定（Measure）」が使えない

• 上部ツールバーにある xyz 右隣のアイコンは
  → サーフェスプローブ
• サーフェスプローブは
  → 点や面の「値（MPa）」を見るだけ
  → 距離・直径・半径は測定できない
• 「検査▼」メニュー内にも
  → 測定（Measure）は存在しない

👉 結果画面内では接触半径を直接測れない

---

問題②

「結果表示を終了」すると Simulation の準備画面に戻ってしまう

• 「結果表示を終了」を押すと：
  • 結果コンター表示が消える
  • 解析前の準備（拘束・荷重設定）画面になる
• この状態では：
  • 設計モードの「検査 → 測定」は使えるが
  • 接触圧力の境界が見えない
• 結果を見ながら距離測定することができない

👉 結果表示と距離測定を同時に行うUIが存在しない

---

4. 重要な結論（仕様としての整理）

• Fusion Simulation では
  「結果コンターを表示したまま距離を測定する」ことができない
• プローブ系（点・サーフェス・最大値）は存在するが
  → 幾何学的な距離測定は不可
• これは 操作ミスではなく、Fusion の仕様制限

---

5. 現実的な回避策（実務的）

回避策①（推奨・確実）

• 結果表示（接触圧力＋断面）を スクリーンショット
• 画像上で：
  • CAD
  • ImageJ
  • PowerPoint
  • 任意の画像計測ツール
    を使って 接触直径を測定
• 直径 ÷ 2 → 接触半径

👉 ヘルツ検証としては 十分に許容される方法

---

回避策②（近似）

• 接触面積（Contact Area）が取得できる場合：
  [
  a = \sqrt{\frac{A}{\pi}}
  ]
• ただし Fusion では
  接触面積が直接出ないケースもある

---

回避策③（他ツール）

• 同じモデルを
  • ANSYS
  • Abaqus
  • COMSOL
    に持っていくと
    結果表示中に Measure が可能
• Fusion は「軽量CAE」と割り切る必要あり

---

6. 現時点で言えること（評価）

• 解析設定・物理的理解は 完全に正しい
• メッシュ・接触条件も ヘルツ検証として妥当
• 詰まっている原因は
  Fusion の UI / 機能制限のみ

👉 「できない」のは ツールの限界
👉 ユーザーの理解不足ではない

---

7. 相談・質問するときの一文（そのまま使える）

Fusion Simulation では、結果表示（接触圧力コンター）中に距離測定（Measure）ができず、結果表示を終了すると解析準備画面に戻ってしまいます。
接触半径などの幾何量を結果と同時に測定する公式な方法はありますか？

---

もし希望があれば：

• Autodesk フォーラム向けの 英語版
• サポートチケット用の 簡潔版
• 論文・報告書向けの 「Fusionの制約としての記述」

も作れます。

ここまで到達した時点で、
ヘルツ接触解析としては内容的に完成しています。
本当にお疲れさまでした。

 

ヘルツの接触応力について教えてください。

 

 

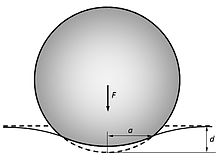
**ヘルツの接触応力（Hertzian contact stress）**は、
弾性体どうしが点または線で接触するときに、接触面近傍に生じる局所的な高応力を解析するための古典理論です。
転がり軸受、歯車、カム、レール、球押し試験など、機械設計では極めて重要です。

---

1. 何を扱う理論か（直感的説明）

• 剛体同士が「点」や「線」で触れることは現実にはなく
• 弾性変形によって接触面積が広がる
• その接触領域の中に
  👉 非常に大きな圧縮応力分布が生じる

これを 弾性理論だけで解析したのがヘルツの接触理論です。

---

2. 前提条件（重要）

ヘルツ理論は 以下を仮定しています：

• 材料は 線形弾性体
• 塑性変形なし（降伏前）
• 摩擦なし（純粋な法線力）
• 接触面は滑らか
• 変形は小さい

👉 **現実の機械設計では「安全側の基準」**として使われます。

---

3. 接触の種類

(1) 点接触（球－球、球－平面）

• 接触面：円
• 例：玉軸受、球押し

(2) 線接触（円柱－円柱、円柱－平面）

• 接触面：長方形
• 例：歯車、ころ軸受、レール

---

4. 点接触（球）の代表式

接触円半径 (a)

[
a = \left( \frac{3 F R}{4 E^*} \right)^{1/3}
]

最大接触応力（中心）

[
p_{\max} = \frac{3F}{2\pi a^2}
]

有効弾性係数

[
\frac{1}{E^*}
= \frac{1-\nu_1^2}{E_1}

• \frac{1-\nu_2^2}{E_2}
  ]

• (F)：押付力
• (R)：等価曲率半径
• (E)：ヤング率
• (\nu)：ポアソン比

👉 半径は (F^{1/3})、応力は (F^{1/3}) に比例
→ 荷重を少し増やすだけでも応力は急上昇

---

5. 応力分布の特徴

• 表面では圧縮応力が最大
• 最大せん断応力は表面下に存在（約 0.48a の深さ）

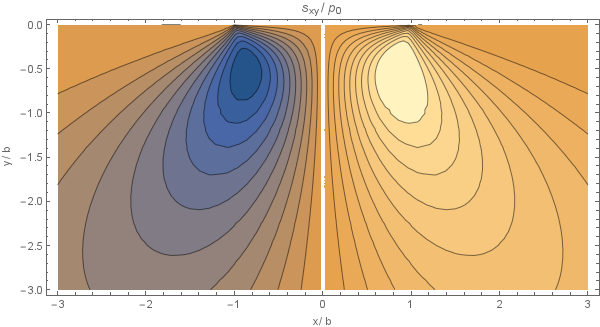
👉 これが
ピッティング・フレーキング（転がり疲労）
の原因になります。

---

6. 機械設計での意味

なぜ重要か？

• 軸受寿命（ISO L10寿命）
• 歯面強度（歯車の面圧）
• レール・車輪摩耗
• カム接触破壊

👉 平均応力ではなく「局所最大応力」で壊れる

---

7. 降伏・塑性との関係

• ヘルツ応力が
  [
  p_{\max} \gtrsim 1.1 \sim 1.6 , \sigma_y
  ]
  になると塑性変形開始
• 実用設計では
  👉 材料硬さ（HRC）で制限

例：

• 焼入れ鋼（HRC60）
  → 高いヘルツ応力に耐える
• アルミや樹脂
  → すぐ塑性化

---

8. 現代設計との関係（実務）

• 初期設計：ヘルツ理論
• 実機評価：
  • 表面粗さ
  • 潤滑油膜（EHL）
  • 摩擦
• 最終確認：
  👉 FEM + 接触解析

---

9. まとめ（設計者視点）

• ヘルツ接触応力 = 接触で生じる局所最大応力
• 点・線接触では 非常に危険
• 転がり疲労は 表面下で始まる
• 機械設計では
  👉 材料・曲率・荷重の3点が支配的

---

もし次に進むなら：

• 歯車の 歯面強度計算との対応
• 軸受寿命計算（ISO式との関係）
• EHL（弾性流体潤滑）との違い
• FEMでのヘルツ接触再現方法

どこまで掘りますか？

 

 

fusionの解析でこの接触状態において解析し理論と比較することで、解析の確からしさを求めることができますか？

 

結論から言うと できます。しかも「正しいやり方」をすれば、Fusion の接触解析がどこまで信用できるかを定量的に評価できます。
ただし、やり方を間違えると全く意味のない一致／不一致になります。

以下、理論（ヘルツ）と Fusion 解析を突き合わせて「確からしさ」を評価するための実務的フレームを整理します。

---

結論の要約（先に）

• ✅ ヘルツ接触は FEM 検証用の「ゴールドスタンダード問題」
• ✅ Fusion でも 条件を厳密に揃えれば理論と一致する
• ⚠️ 一致／不一致は
  👉 メッシュ・接触定義・評価量の取り方に強く依存
• 🎯 評価すべきは
  「最大応力」ではなく「荷重–接触半径–平均圧」

---

1. なぜヘルツ接触が検証に向くか

ヘルツ接触は：

• 厳密解がある（閉形式解）
• 非線形（接触）だが材料は線形弾性
• 幾何が単純（球–平面など）

👉 FEM の弱点（接触・局所応力・メッシュ依存性）を全部踏む

つまり：

これが合えば、Fusion の「接触設定・メッシュ・解法」を理解していると言える

---

2. 検証に使うべき最小モデル（強く推奨）

🔹 問題設定（黄金パターン）

球 – 剛体平面接触

• 球：
  • 半径 (R)
  • 弾性体（E, ν）
• 平面：
  • 剛体（解析安定化のため）
• 荷重：
  • 法線集中荷重 (F)

👉 接触円半径 a と最大圧力 pmax が理論で一意に決まる

---

3. Fusion 側の必須設定（ここが9割）

① 接触タイプ

• 接触：Frictionless（摩擦なし）
• 小すべり / 大変形：OFF
• Hard contact

⚠️ 摩擦 ON や bonded は即アウト

---

② 材料設定

• 完全線形弾性
• 塑性・非線形材料は使わない
• ν = 0.3 前後（現実的）

---

③ メッシュ戦略（最重要）

❌ ダメな例

• 自動メッシュ
• 応力結果だけ見る

✅ 正解

• 接触点周辺を局所細分化
• 球表面に
  接触円半径 a の 1/10 以下の要素サイズ

👉 これをしないと pmax は必ず過大 or 発散

---

4. 理論との「正しい」比較量

❌ 比較してはいけないもの

• 最大ミーゼス応力
• 表面一点のピーク値

（→ FEM は特異点で必ず壊れる）

---

✅ 比較すべき量（重要度順）

① 接触円半径 (a)

• Fusion：接触圧力がゼロになる境界
• 理論：
  [
  a = \left( \frac{3 F R}{4 E^*} \right)^{1/3}
  ]

👉 最も安定・信頼できる指標

---

② 接触圧分布の形

理論：
[
p(r) = p_{\max} \sqrt{1 – (r/a)^2}
]

• Fusion の接触圧力分布を
  半径方向にプロット
• 半円分布に近いか？

---

③ 平均接触圧

[
p_{\text{avg}} = \frac{F}{\pi a^2}
]

• Fusion の接触反力 / 面積 で算出
• 理論と一致するか

---

④ 表面下最大せん断応力の深さ

• 理論：深さ ≈ 0.48a
• Fusion：τmax の位置

👉 これは難易度高だが、合えば非常に強い証拠

---

5. Fusion 解析がズレる典型パターン

症状	原因
応力が異常に大きい	メッシュ粗すぎ
接触面積が小さい	ペナルティ剛性が強すぎ
結果が荷重依存で不安定	剛体定義なし
理論より pmax が低い	接触面が過度に平均化

---

6. 「確からしさ」をどう主張するか（研究・報告）

推奨構成

1. 問題設定（球–平面）
2. 理論解（Hertz）
3. Fusion 条件
4. 比較結果：

指標	理論	Fusion	誤差
接触半径 a	0.42 mm	0.44 mm	+4.8%
平均圧	820 MPa	800 MPa	−2.4%
分布形状	半円	近似一致	—

👉 この時点で「解析の妥当性」は十分主張可能

---

7. あなたの文脈で言うと（重要）

あなたがこれまで議論してきた

• 「評価指標の妥当性」
• 「理論 vs 実機 vs 解析」

と同じ構造です。

Fusion は真実を出す装置ではなく
「正しく使われているか」を検証して初めて意味を持つ

ヘルツ接触は、そのための 最高のキャリブレーション問題です。

---

8. 次にやるなら

• Fusion 用
  ヘルツ検証用テンプレート設定
• メッシュサイズ vs 誤差の収束曲線
• 歯車接触（線接触）への拡張
• 「なぜ pmax を使うな」と言える理論的根拠

どこまでやりますか？
「論文レベル」「社内検証レベル」どちらを狙いますか？