モールの応力円
モールの応力円とは
モールの応力円は、外力に対して、内部でどういう力が発生したのかが
ビジュアル的に把握できるという代物です。
参考:
モールの応力円とは?意味と書き方を、計算をすっとばして説明するよ【超初心者向け】
モールの応力円の公式
モールの応力円では、主応力$σ_1$、$σ_2$が与えられたとき
θだけ傾いた面で働いている力を求める事ができます。
モールの応力円の式は
$(σ_x^{ ’ }-\frac{σ_x+σ_y}{ 2 })^{ 2 }+τ^{ 2 }_{x^{ ’ }y^{ ’ }}=\frac{ 1 }{ 4 }(σ_x-σ_y)^{2}++τ^{ 2 }_{xy}$
となります。
これは、中心座標が[$\frac{σ_x+σ_x}{ 2 }$,0]で
半径が$(\frac{ 1 }{ 4 }(σ_x-σ_y)^{2}++τ^{ 2 }_{xy})^{0.5}$の円を表しています。
おすすめ例題
Q1:https://www.noboyu.com/entry/Mohrs-circle
Q2:http://civil.meijo-u.ac.jp/lab/kodaka/lecture07/no11.pdf
応力のつり合いとひずみと変位
応力のつり合い方程式
下の図のような微小物体内では、
垂直応力$σ_x$、$σ_y$、$σ_z$
せん断応力$τ_{xy}$、$τ_{xz}$、
物体力X、Y、Zが作用するとき、
x、y、z方向のつり合いを考えると、
$\frac{∂σ_x}{ ∂x }+\frac{∂τ_{xy}}{ ∂y }+\frac{∂τ_{zx}}{ ∂z }+X$
$\frac{∂τ_{xy}}{ ∂x }+\frac{∂σ_{y}}{ ∂y }+\frac{∂τ_{yz}}{ ∂z }+Y$
$\frac{∂τ_{zx}}{ ∂x }+\frac{∂τ_{yz}}{ ∂y }+\frac{∂σ_{z}}{ ∂z }+Z$
これを応力のつり合い方程式という。
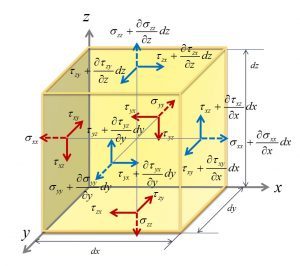
図の引用:https://gijutsuya.net/knowledge-base/1847/
ひずみ-変位関係式
$ε_x = \frac{∂u}{ ∂x }$
$ε_y = \frac{∂v}{ ∂y }$
$ε_z = \frac{∂w}{ ∂z }$
$γ_{xy} = \frac{∂u}{ ∂y }+\frac{∂v}{ ∂x }$
$γ_{yz} = \frac{∂v}{ ∂z }+\frac{∂w}{ ∂y }$
$γ_{zx} = \frac{∂w}{ ∂x }+\frac{∂u}{ ∂z }$
ここで、$ε_x$、$ε_y$、$ε_z$はそれぞれx、y、z軸方向の垂直ひずみ、
$γ_{xy}$、$γ_{yz}$、$γ_{zx}$はそれぞれx-y面、y-z面、z-x面のせん断ひずみであり
これらをまとめてひずみ成分という。
また、x、y、z軸まわりの変形を伴わない回転の角度は
$ω_{x} = \frac{1}{2}(\frac{∂w}{ ∂y }-\frac{∂v}{ ∂z })$
$ω_{y} = \frac{1}{2}(\frac{∂u}{ ∂z }-\frac{∂w}{ ∂x })$
$ω_{z} = \frac{1}{2}(\frac{∂v}{ ∂x }-\frac{∂u}{ ∂y })$
で表される。これらを回転(rotation)という。
ひずみ適合条件式
前述した、「ひずみ-変位関係式」から変位成分を消去すると、
ひずみ成分が満たすべき条件が次の式のように求められる。
$\frac{∂^{2}ε_x}{ ∂y^{2} }+\frac{∂^{2}ε_y}{ ∂x^{2} }= \frac{∂^{2}γ_{xy}}{ ∂x∂y }$
$\frac{∂^{2}ε_y}{ ∂z^{2} }+\frac{∂^{2}ε_z}{ ∂y^{2} }= \frac{∂^{2}γ_{yz}}{ ∂y∂z }$
$\frac{∂^{2}ε_z}{ ∂x^{2} }+\frac{∂^{2}ε_x}{ ∂z^{2} }= \frac{∂^{2}γ_{zx}}{ ∂z∂x }$
$2\frac{∂^{2}ε_x}{ ∂y∂z }= \frac{∂}{∂x}(-\frac{∂γ_{yz}}{ ∂x }+\frac{∂γ_{zx}}{ ∂y }+\frac{∂γ_{xy}}{ ∂z })$
$2\frac{∂^{2}ε_y}{ ∂z∂x }= \frac{∂}{∂z}(\frac{∂γ_{yz}}{ ∂x }-\frac{∂γ_{zx}}{ ∂y }+\frac{∂γ_{xy}}{ ∂z })$
$2\frac{∂^{2}ε_z}{ ∂x∂y }= \frac{∂}{∂z}(\frac{∂γ_{yz}}{ ∂x }+\frac{∂γ_{zx}}{ ∂y }-\frac{∂γ_{xy}}{ ∂z })$
これらをひずみの適合条件といい、ひずみ成分がこの条件を満たすときにのみ変位が一義的に定められる。
この式はつまり
ひずみの独立な成分は6個[εxx,εyy,εzz,εxy、εxz,εyz]
変位は3つ。[ux,uy,uz]
ひずみと変位の関係式
εij=[∂iuj+∂jui]/2
の6個
問題を変位で表した式を解いて、変位が求まった場合には、その後にひずみを求めるならこの式をつかって、計算できる。
応力ひずみ関係から問題を解いてひずみが求まった場合、
ひずみの6成分があたえられたとき、変位の3つの未知数を6個の式で求めることになり、任意のひずみからは、変位を求められない。すなわち、
ひずみに条件が必要。
物理的には、もともとおなじ位置が変位(変形)後にもおなじ位置にいる条件。
通常、3つの条件があればいいが、独立でない3つを加えて、6個の式で表す。
おすすめ例題
[理解度アップ]
http://www.geol.tsukuba.ac.jp/~yagi-y/text/2015geody-resources.pdf
http://aitech.ac.jp/~narita/telastic01.pdf
[肩慣らし]
http://web.tuat.ac.jp/~nagaki/zairiki/exercise/ex2007/2k7ze01_Bans.pdf
http://ms-laboratory.jp/zai/ex_z/ex_1.htm
[飛ばしたけど必要かもしれない内容]
・応力・ひずみの座標変換
弾性問題
[おすすめ例題]
http://aitech.ac.jp/~narita/telastic02.pdf
http://www.jsce.or.jp/committee/amc/compmech/pdftext121204/saiki.pdf
【本気でおすすめの工学便覧】
一緒に便覧を使って勉強していきませんか。
エンジニアや工学部学生は勿論のこと、頭の体操をしたい大人にもうってつけです。
頭の体操に用いられている問題は、工学便覧を順番に解いています。
この便覧はホントにやばいです。
紙の本で全巻揃えようと思うと、多分10万円位かかると思います。
DVD版なら1万円以下。値段と置き場所を考えたら、絶対にお買い得。
みんなに勧めたくなくレベルでコスパが良すぎる。
 図の引用:https://gijutsuya.net/knowledge-base/1847/
図の引用:https://gijutsuya.net/knowledge-base/1847/