 $\quad \varepsilon_1 = \frac{P_1}{AE}, \quad \varepsilon_2 = \frac{P_2}{AE}$
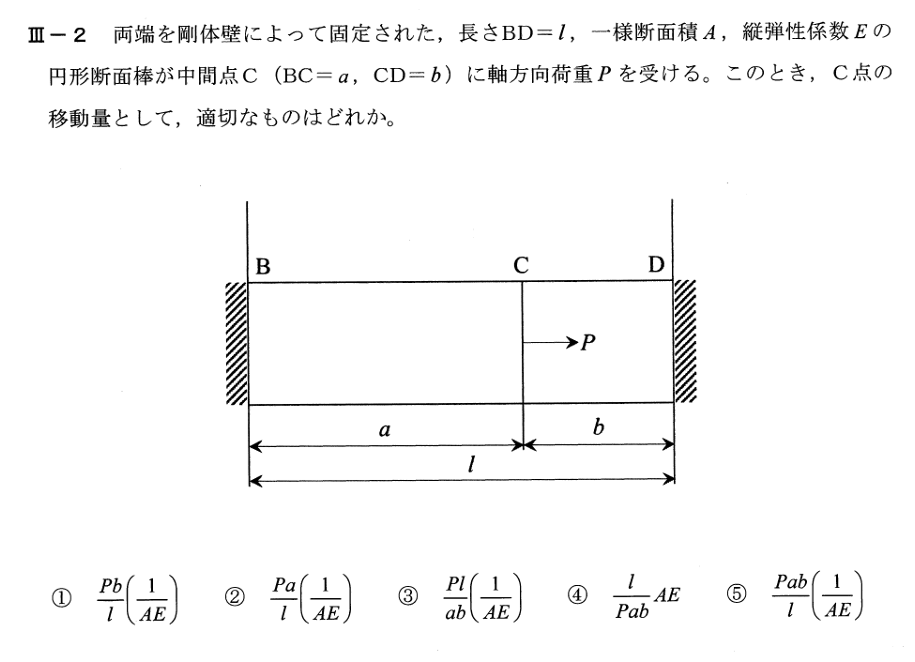
棒の両端は拘束されているから,2つの棒に生じる伸びの和は0となる。
$\lambda_1 + \lambda_2= 0, \quad \therefore \frac{P_1 a}{AE} + \frac{P_2 b}{AE} = 0$
軸力と外力の間には
$P = P_1 – P_2$
の関係が成り立つので、
$P_1 = \frac{ b}{ l} P, \quad P_2 = -\frac{a}{l} P$
荷重Pの作用点における変位λは
$\lambda = \lambda_1 = \frac{P a b}{l}(\frac{1}{AE})$
[解答]⑤
参考
第2回 引張と圧縮
棒の伸び 引張り強さ(H26)
材料力学 自重による段付き棒の伸び(H25)
$\quad \varepsilon_1 = \frac{P_1}{AE}, \quad \varepsilon_2 = \frac{P_2}{AE}$
棒の両端は拘束されているから,2つの棒に生じる伸びの和は0となる。
$\lambda_1 + \lambda_2= 0, \quad \therefore \frac{P_1 a}{AE} + \frac{P_2 b}{AE} = 0$
軸力と外力の間には
$P = P_1 – P_2$
の関係が成り立つので、
$P_1 = \frac{ b}{ l} P, \quad P_2 = -\frac{a}{l} P$
荷重Pの作用点における変位λは
$\lambda = \lambda_1 = \frac{P a b}{l}(\frac{1}{AE})$
[解答]⑤
参考
第2回 引張と圧縮
棒の伸び 引張り強さ(H26)
材料力学 自重による段付き棒の伸び(H25)
区間軸力について教えて下さい
区間軸力(internal axial force)とは、 棒のある区間内部に生じている軸方向の力(引張または圧縮) のことです。 外力を受けると内部に「見えない力」が生じ、それが棒の伸び・縮みを決めます。 今回の問題は、この 区間 BC の軸力 (N_L) と 区間 CD の軸力 (N_R) が登場しました。 これがどうやって決まり、どんな意味を持つのかを、ゆっくり丁寧に説明します。✅ 1. 区間軸力とは?
棒の任意の場所で「切断して」考えたとき、その切断面に現れる内部力のことです。 例えば区間 BC を切ると、切断面に次のような力が現れます:- 引張方向に働くなら 引張軸力(伸ばす力)
- 圧縮方向に働くなら 圧縮軸力(縮める力)
✅ 2. 今回の棒の特殊な状況
棒は 両端が完全固定 されています。[壁]—(BC)—C—(CD)—[壁]
↑
P(右向き)
- 左側の BC 区間は引っ張られる(右端 C が引かれる)
- 右側の CD 区間は押しつぶされる(C が壁側を押す格好)
- 左区間:引張軸力 (N_L)
- 右区間:圧縮軸力 (N_R)
✅ 3. つり合いで求まる関係
節点 C の水平つり合いより [ N_L + N_R = P ] これは単純で、右へ P の外力を支えるため、内部は左右に分担して支える、という式です。✅ 4. もうひとつ重要な方程式(変位の一致=適合条件)
C の変位は- 左区間 BC の伸び
- 右区間 CD の縮み(符号は逆だが変位としては右へ動く)
✅ 5. この2式を連立すると区間軸力が決まる
[ \begin{cases} N_L + N_R = P \ N_L a = N_R b \end{cases} ] 解くと [ N_L = \frac{Pb}{l},\qquad N_R=\frac{Pa}{l} ]✅ 6. 区間軸力の物理イメージ
- 荷重点に近い側ほど大きな軸力を負担
- 荷重点から遠い側は比較的小さな軸力
✅ 7. 全体まとめ(区間軸力とは?)
- 外力を受けた棒を切断すると現れる「内部の引張・圧縮力」
- その値は つり合い条件 と 変形(適合)条件 の両方で決まる
- 伸びや縮みの計算には [ \Delta = \frac{NL}{AE} ] で使われる
- 両端固定のような構造では、区間ごとに軸力が違うのが普通
必要なら ✅ この棒の内力図(軸力図) ✅ 組み合わせ応力との関係 ✅ 固定支持とピン支持の違い なども説明できます。
N_L a = N_R bは適合条件の式変形をしたのですね
はい、その理解で完全に正しいです!✅ 結論
[ \boxed{N_L,a = N_R,b} ] この式は 変位の適合条件(compatibility) [ \frac{N_L a}{AE}=\frac{N_R b}{AE} ] を AE を消して整理しただけ です。 つまり、C 点の変位は、左区間の伸び量と右区間の縮み量が一致する → その条件式を整理すると [ N_L a = N_R b ]となる、ということです。
✅ 変位の適合条件 → N_L a = N_R b が生まれる流れ
- 両端固定だから
C 点の変位は
- 左側の伸び
- 右側の縮み が「同じ距離」でなければならない。
- 材料力学の伸び縮みの式: [ \Delta = \frac{N L}{AE} ]
- 左右の変位を等しいと置く: [ \frac{N_L a}{AE}=\frac{N_R b}{AE} ]
- AE を消すと: [ \boxed{N_L a = N_R b} ]
✅ さらに深い理解のための要点
- 不静定構造は、力のつり合い式だけでは内部力(N_L, N_R)が決まらない。
- 必ず 変形の一致(適合・compatibility) を使う。
- その適合条件が、結果として [ N_L a = N_R b ] という非常にシンプルな関係式を生み出す。
✅ 直感も合っている
- 長さ a 側は柔らかいので “小さい軸力” しか分担できない
- 長さ b 側は硬いので “大きい軸力” を分担する
- その比が「長さの逆比」になって現れる [ \frac{N_L}{N_R}=\frac{b}{a} ]
必要なら、
- カスティリアノの定理で同じ式を導く方法
- 内力図(N図)の描き方
- 両端固定と片端固定での違い なども説明できます!