技術士 過去問 平成27年度（2015年） 問17　異材結合棒の変位を極める！ヤング率の違いが生む応力バランスの妙

https://kakomonn.com/gijyutushi/questions/36516

https://www.engineer.or.jp/c_topics/007/attached/attach_7462_1.pdf

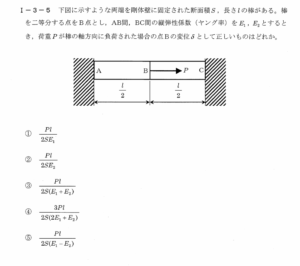
下図のように、両端を剛体壁に固定された長さ $l$、断面積 $S$ の棒を考え、棒を二等分する点を $B$ とします。左半分（区間 $AB$）のヤング率を $E_1$、右半分（区間 $BC$）のヤング率を $E_2$ とし、軸方向に荷重 $P$ をかけたときの点 $B$ の変位 $\delta$ を求めます。

固定――――A――――B――――C――――固定
      ←l/2→  ←l/2→
      E1      E2

１．各部材の変位

区間 $AB$（長さ $L = l/2$）に働く内力を $P_A$、区間 $BC$ に働く内力を $P_B$ とします。

• 部材 AB の縦ひずみ
  応力 $\sigma_A = P_A / S$
  ひずみ $\displaystyle \varepsilon_A = \frac{\sigma_A}{E_1} = \frac{P_A}{S E_1}$
  変位（伸び）

  $$\delta_A = L\,\varepsilon_A = \frac{l}{2}\,\frac{P_A}{S E_1} = \frac{l\,P_A}{2 S E_1}.$$

• 部材 BC の縦ひずみ
  応力 $\sigma_B = P_B / S$
  ひずみ $\displaystyle \varepsilon_B = \frac{\sigma_B}{E_2} = \frac{P_B}{S E_2}$
  変位（縮み方向だが絶対値で扱う）

  $$\delta_B = L\,\varepsilon_B = \frac{l}{2}\,\frac{P_B}{S E_2} = \frac{l\,P_B}{2 S E_2}.$$

２．力の釣り合いと変位互換

1. 力の釣り合い：外からの荷重 $P$ は、内部で $P_A$ と $P_B$ に分かれるため

   $$P = P_A + P_B.$$

2. 固定端条件：両端が動かないので、左部材の伸び $\delta_A$ と右部材の縮み $\delta_B$ が同じだけ起こり、互いに打ち消し合います。

   $$\delta_A = \delta_B.$$

３．未知 $P_A,\,P_B$ の解法

$$\frac{l\,P_A}{2 S E_1} = \frac{l\,P_B}{2 S E_2} \quad\Longrightarrow\quad \frac{P_A}{E_1} = \frac{P_B}{E_2} \quad\Longrightarrow\quad P_B = P_A\frac{E_2}{E_1}.$$

これを $P = P_A + P_B$ に代入して

$$P = P_A\Bigl(1 + \tfrac{E_2}{E_1}\Bigr) \quad\Longrightarrow\quad P_A = \frac{E_1}{E_1+E_2}\,P, \quad P_B = \frac{E_2}{E_1+E_2}\,P.$$

４．点 $B$ の変位

$$\delta \;=\;\delta_A \;=\;\frac{l\,P_A}{2 S E_1} \;=\;\frac{l}{2S E_1}\;\frac{E_1}{E_1+E_2}\,P \;=\;\boxed{\frac{P\,l}{2\,S\,(E_1+E_2)}}.$$

これが正解（選択肢③）となります (kakomonn.com)。