材料力学
内力と外力の関係を教えて下さい
もちろん、材料力学における内力と外力の基本的な関係について説明します。
外力：これは物体に外から作用する力です。例えば、棒や梁にかかる荷重や支点にかかる反力などが考えられます。
内力：物体の内部で、外力や境界条件の影響を受けて生じる力です。内力は、物体が破壊されないように外力をバランスさせる役割があります。例えば、引張りや圧縮、せん断、曲げ、ねじれなどの力が考えられます。
外力と内力の関係：
外力と内力の関係は、物体の静的平衡を考えることで理解できます。外からの力（外力）が作用すると、物体はその力に抵抗するための力（内力）を発生させます。物体が静的平衡状態にある場合、外力と内力は等しく、反対向きに作用します。これにより、物体は破壊されずに平衡を保つことができます。
例えば、両端が固定された梁に荷重がかかると、梁はその荷重に抵抗するための曲げモーメントやせん断力などの内力を発生させます。これらの内力は、外力によって引き起こされる変形や応力をバランスさせる役割があります。
このように、材料力学では、物体の内部で生じる内力と外部からの外力との関係を詳しく研究することで、物体の強度や変形の挙動を理解し、設計や評価を行います。
機械力学・制御
制御における特性方程式と伝達関数の違いを教えてください
フルビッツの安定判別法
フルビッツの安定判別法を使う前に以下の2点に注意
・係数はすべて正の値である
・多項式の各次数に項が存在する
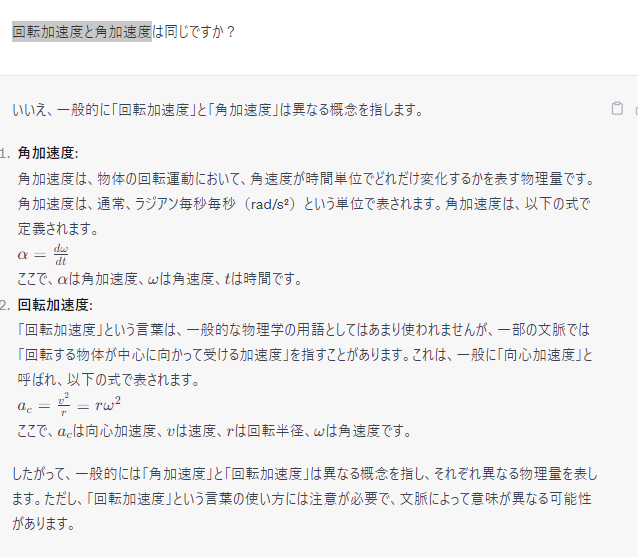
回転加速度と角加速度は同じですか？
熱工学
流体工学
抗力係数
抗力係数が1以上になる場合を教えてください
抗力係数が1以上になる場合は、特に非流線型の物体や一部の流れの条件において見られます。以下は、抗力係数が1以上になる典型的な例です：
円柱：円柱が流れに対して直角に置かれると、背後に大きな乱流の渦が形成されるため、抗力係数は1を大きく超えることが一般的です。
球形の物体：特定のレイノルズ数の範囲で、球の抗力係数は1を超えることが知られています。
平板：流れ方向に対して直角に置かれた平板は、流れの前面で大きな乱流を生じるため、抗力係数は非常に大きくなります。
角のある物体：鈍角や直角のエッジを持つ物体は、エッジの部分で流れが分離しやすく、これが大きな抗力を生じる原因となります。
複雑な形状の物体：多くの突起や凹凸を持つ物体や、非常に複雑な形状の物体は、流れの乱れを引き起こしやすく、これが抗力の増大を招くことがあります。
これらの物体や条件は、流れの中で大きな乱流や渦を生じやすく、それが抗力の増大を招く主な原因となります。抗力係数が1以上となる場合は、特に流れの分離や渦の形成が顕著であることが多いです。
理想気体の密度方程式というものもあるのですか？
流体力学での微分の意味を教えて下さい
流体力学における微分は、流体の変化やその動きを数学的に表現する際に使用されます。以下に、流体力学における微分の主な意味や用途を説明します。
変位の微分: 流体の速度を表現するために、位置の変化を時間で微分します。たとえば、流速
vは位置の微分として得られます。
速度の微分: これは流体の加速度を示しています。速度の時間的な変化（時間での微分）は、外力や圧力勾配などの影響を受ける場合の流体の反応を示すことができます。
連続の方程式: 流体の質量が保存されるという原理を表現します。これは流体の密度の時間的変化と流速の空間的変化の微分を組み合わせることで導かれます。
ナビエ–ストークス方程式: これは流体の運動を表現する主要な方程式です。圧力、粘性、外力などの要因による速度の変化を表すために、速度の微分が使用されます。
変数の変化: 流体中の温度や濃度などの物理的、化学的な変数の変化を記述するために、時間や空間での微分が使用されます。
これらは流体力学の基本的な概念の一部に過ぎませんが、微分は流体の動きやその他の物理的特性を理解し、数学的に記述するための重要なツールです。
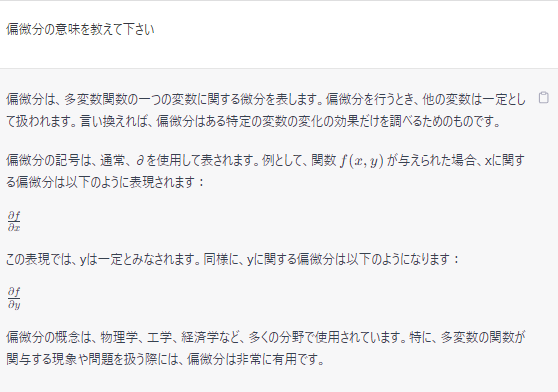
偏微分の意味を教えて下さい
