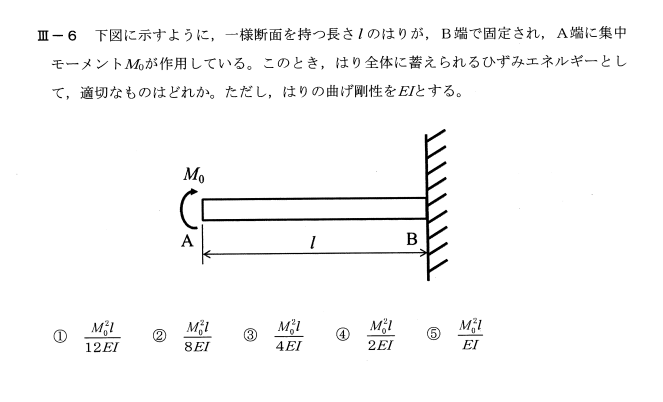
【問題】(pdfファイル)
ダウンロードして使用してください。
問題と解答
問題1
真空中にある半径1cmの導体球に1×10
-6Cの電荷を与えた。ただし
,電荷はすべて導体球の球表面に集中しており
,導体球の外側の電界は
,全電荷が球の中心にあるものとして考えればよい。
(1
)球の中心からの距離x[
m]だけ離れた点の電界の大きさE[
V/m]とする。横軸x,縦軸Eのグラフをかけ。

(2
)次の(a)~(c)の事項のうち
,正しいものをすべて選び
,記号で答えよ。
- 電束密度は,空間の誘電率に反比例する。
- 電界の大きさは,空間の誘電率に反比例する。
- 電気力線は,等電位面に垂直に交わる。
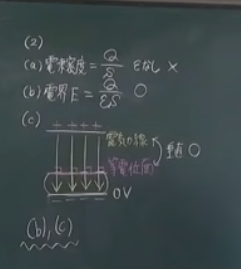
問題2
真空において
,xy平面上の点A(-1,0)点B(1,0)のそれぞれに大きさ2.0×10
-6[
C]の正の点電荷を置く。
真空の誘電率を8.85×10
-12[
F/m]として
,以下の問いに答えよ。
(1
)点C(0,1)における電界の強さ[
V/m]を求めよ。解答は
,単位をつけて答えること。

(2
)点C(0,1)における電位[
V]を求めよ。解答は
,単位をつけて答えること。
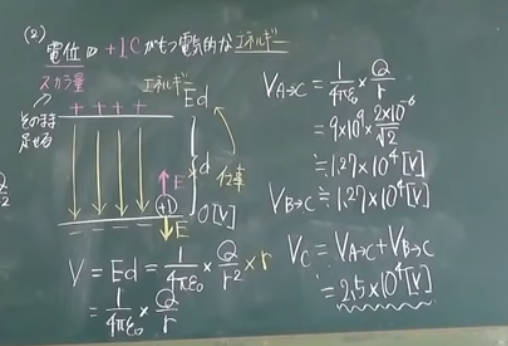
問題3
真空中において
,同一直線上の点A,Bのそれぞれに大きさ2.0×10
―6[
C],3.0×10
―6[
C]の正電荷を置いた。
このとき
,AB間の中間地点の電界の大きさは
,1×10
5[
V/m]であった。このとき
,AB間の距離[
m]を求めよ。
ただし
,真空の誘電率ε0 = 8.85×10
-12[
F/m]とする。
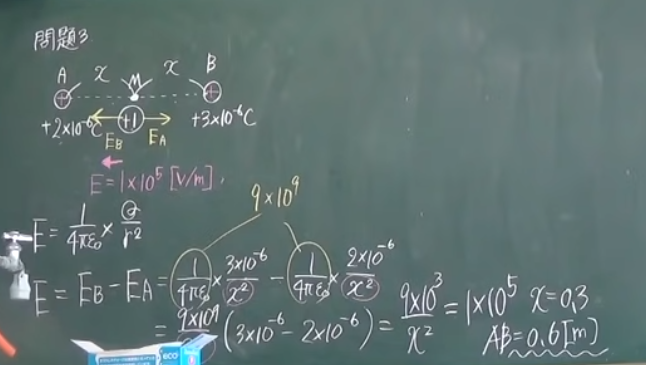
問題4
図のように
,極板間が真空で
,その距離がd[
m]のコンデンサに
,極板面積S[
m2]と同じ面積をもつ導体と比誘
電率3の誘電体を挿入する。極板間の電位差がV[
V]であり
,極板間距離が真空
,導体
,誘電体の3空間に等分されているとき
,以下の問いに答えよ。
(1
)真空部分
,導体部分
,誘電体部分の電位差[
V]をV真空,V導体,V誘電体とすると
,V真空:V導体:V誘電体を求めよ。
(2
)真空部分
,導体部分
,誘電体部分の電界の大きさ[
V/m]をそれぞれ求めよ。
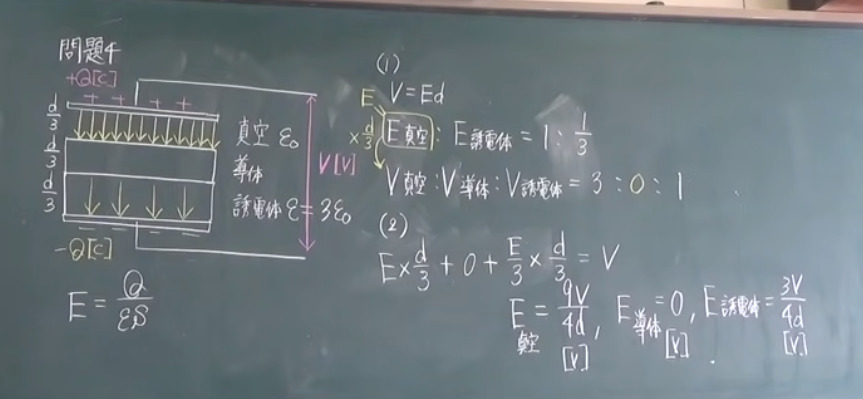
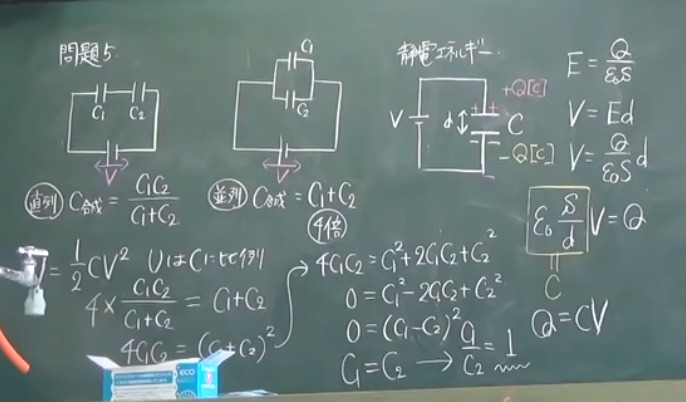
問題5
電気容量C1[
F],C2[
F]の2つのコンデンサがある。これら2つのコンデンサを直列に接続した場合と
,並列に
接続した場合で
,同じ電源を用いて十分に充電を行った。すると
,並列に接続した場合の方が
,直列に接続した場合よりも4倍の静電エネルギーを蓄えることができた。
C1/C2 の値を求めよ。
問題6
図のように
,極板面積がS[
m2],極板間距離d[
m]のコンデンサA,BがスイッチSWと抵抗R[Ω]を介して連
結してある。コンデンサAの極板間は真空であり,その電気容量は2[μF]である。一方で,コンデンサBの極
板間の空間は上下に二等分されており
,上半分は真空
,下半分は比誘電率3の誘電体で満たされている。はじめ
,
スイッチSWを開いた状態で
,Aには1[μC]の電荷が蓄えられており
,Bには電荷は蓄えられていないものとする。
(1
)コンデンサBの電気容量[μF]を求めよ。
(2
)スイッチSWが開いているときのコンデンサA,Bに蓄えられている
静電エネルギー[μJ]の合計を求めよ。
(3
)スイッチSWを閉じて十分時間が経過すると
,コンデンサBに蓄えら
れている電荷[μC]を求めよ。
(4
)スイッチSWを閉じてから十分時間が経過するまでに抵抗R[Ω]で消費されたエネルギー[μJ]を求めよ。

問題7
図のように
,2つのコンデンサC1,C2を直列につないだ。コンデンサC2の極板
間距離はC1の2倍であるが
,極板面積は等しく
,極板間は両方ともに真空である。
はじめスイッチを閉じて十分に時間が経過した。その後
,スイッチを開き
,コンデ
ンサC2の極板間全体を比誘電率3の誘電体で満たした後
,スイッチを開いたままにした。このとき
,静電エネルギーは
,誘電体の挿入前後で何倍になっているか。
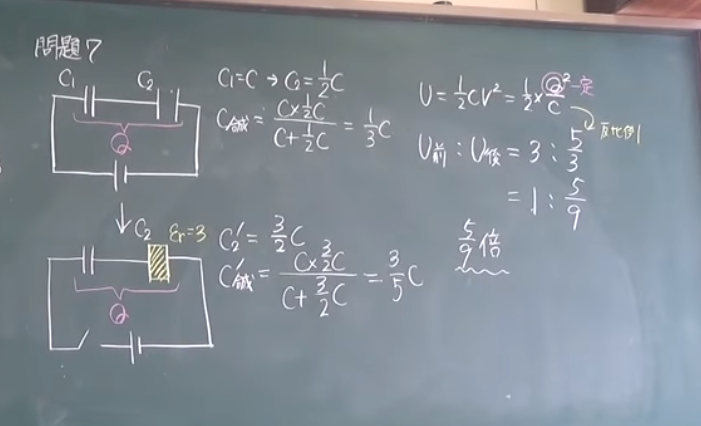
<おすすめ記事>
電験3種 理論のおすすめの勉強先リンク
 (2)次の(a)~(c)の事項のうち,正しいものをすべて選び,記号で答えよ。
(2)次の(a)~(c)の事項のうち,正しいものをすべて選び,記号で答えよ。
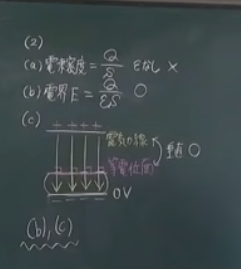
 (2)点C(0,1)における電位[V]を求めよ。解答は,単位をつけて答えること。
(2)点C(0,1)における電位[V]を求めよ。解答は,単位をつけて答えること。
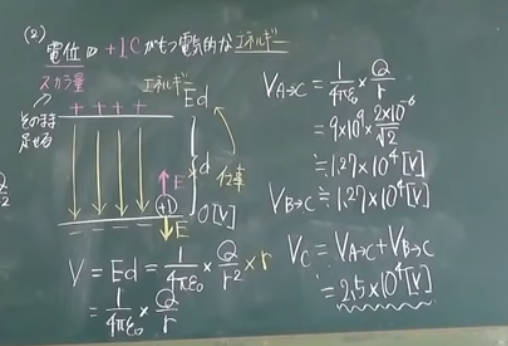
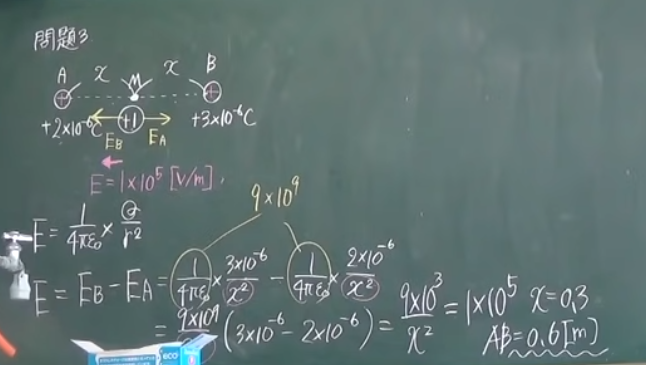
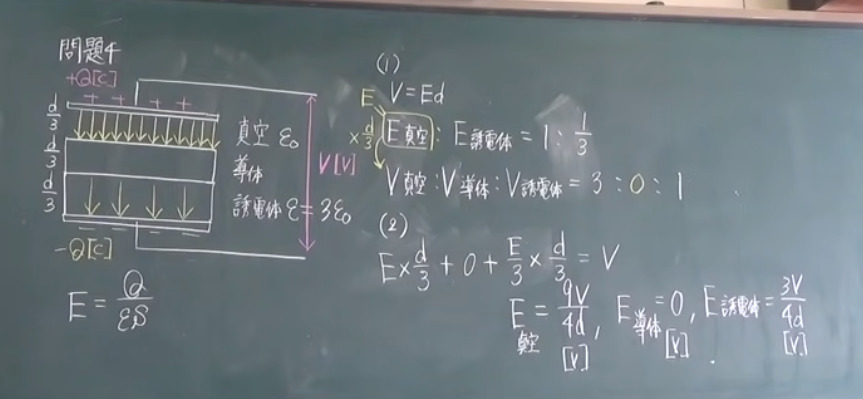


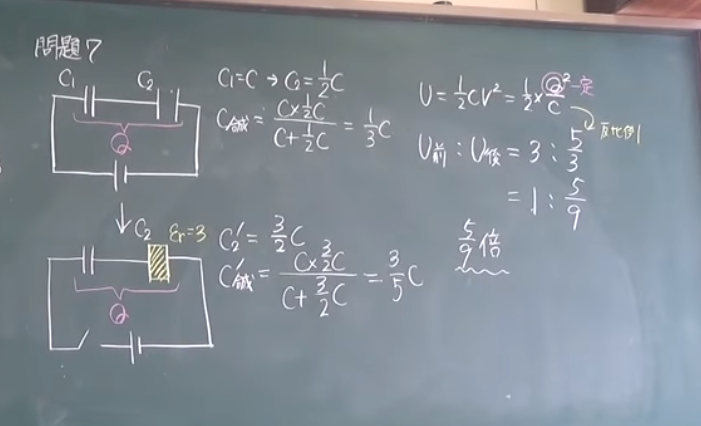 <おすすめ記事>
電験3種 理論のおすすめの勉強先リンク
<おすすめ記事>
電験3種 理論のおすすめの勉強先リンク