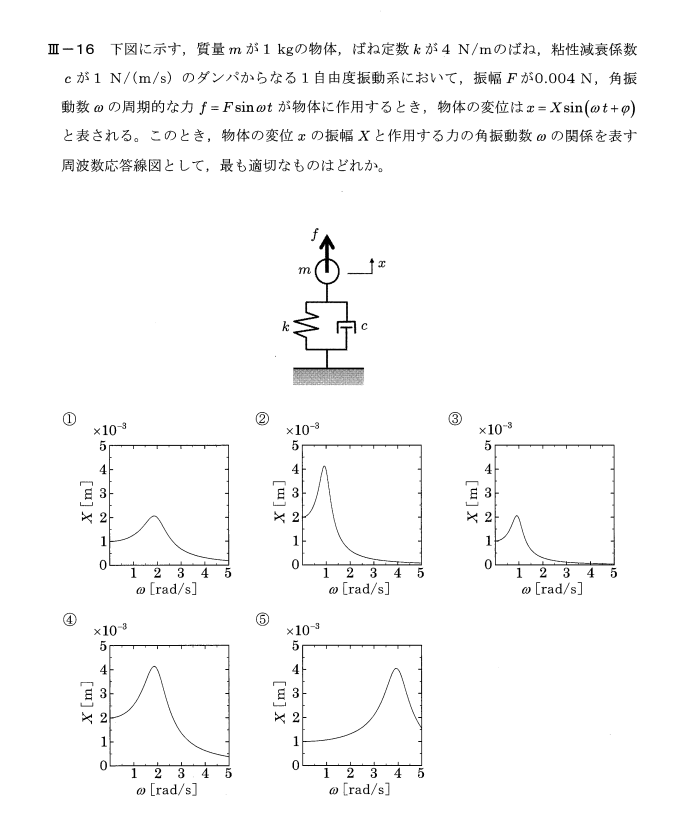
図中の減衰比 ζ は標準定義 ζ=c2mk\zeta=\frac{c}{2\sqrt{mk}}   により求めます。
  • m=10 kgm=10\ {\rm kg}  、 k=1000 N/mk=1000\ {\rm N/m}  、 c=20 Ns/mc=20\ {\rm Ns/m}  なので
2mk=210×1000=210000=2×100=200.2\sqrt{mk} =2\sqrt{10\times1000} =2\sqrt{10000} =2\times100=200. ζ=20200=0.1.\zeta=\frac{20}{200}=0.1.  
よって最も近い選択肢は ③ 0.1 です。   参考：技術士第一次試験－令和2年度機械部門Ⅲ-20解答例 | 技術士のたまご

この問題はcとkが並列で描かれていますが、直列でも同じ解答になりますか？

  標準的な１自由度系 mx¨+c x˙+k x=0m\ddot x + c\,\dot x + k\,x = 0   という形で使った減衰比 ζ=c2mk\zeta=\frac{c}{2\sqrt{mk}}   は，ばね kk とダンパ cc が並列に質量に直結している場合の式です。もしこれらを直列につないで質量に引き付けた場合には，運動方程式そのものが変わり，減衰比の定義も変わってしまいます。

並列接続の場合

  • 運動方程式： mx¨+c x˙+k x=0m\ddot x + c\,\dot x + k\,x =0 
  • 減衰比： ζ=c2mk\displaystyle \zeta=\dfrac{c}{2\sqrt{mk}} 

直列接続の場合

壁―ばね kk ―ダンパ cc ―質量，という順序で直列に並べてみると，力 FF は両素子で共通・変位は足し合わせになります。運動方程式を立てると最後には mx¨+k mc⏟ceff x˙+k x=0m\ddot x + \underbrace{\frac{k\,m}{c}}_{c_{\rm eff}}\,\dot x + k\,x=0   となり，
  • 有効な減衰係数は ceff=k m/cc_{\rm eff}=k\,m/c 
  • よって減衰比は ζseries=ceff2m k=k m/c2m k=m k2 c≠c2m k\zeta_{\rm series} =\frac{c_{\rm eff}}{2\sqrt{m\,k}} =\frac{k\,m/c}{2\sqrt{m\,k}} =\frac{\sqrt{m\,k}}{2\,c} \neq \frac{c}{2\sqrt{m\,k}}と まったく別の式 になります。

まとめ

  • 並列で直結すると cc  ・ kk  がそのまま ODE に現れ， ζ=c/(2mk)\zeta=c/(2\sqrt{mk})  が成り立つ。
  • 直列につなぐと式が変形され，有効減衰係数も k m/ck\,m/c  のように入れ替わるので，同じ解答にはなりません。
したがって「直列でも同じ ζ になるか？」という問いの答えは 「いいえ，変わります」 です。

2m k

 

はなに？

“ 2m k2\sqrt{m\,k} ” は、まさに臨界減衰係数 ccc_c の式です。つまり cc  =  2m kc_c \;=\;2\sqrt{m\,k}   とおくと、減衰比を ζ=ccc=c2m k\zeta=\frac{c}{c_c}=\frac{c}{2\sqrt{m\,k}}   と定義でき、
  • ζ<1\zeta<1  ：不足減衰
  • ζ=1\zeta=1  ：臨界減衰
  • ζ>1\zeta>1  ：過減衰
に分類できます。 由来 運動方程式を mx¨+cx˙+kx=0m\ddot x + c\dot x + kx=0   とすると、特性方程式は s2+cms+km=0.s^2 + \frac{c}{m}s + \frac{k}{m}=0.   この二次方程式の判別式をゼロにして「重根にする」（振動せず最速収束の条件）と (cm)2−4km=0⟹cc=2m k.\Bigl(\tfrac{c}{m}\Bigr)^2 - 4\tfrac{k}{m}=0 \quad\Longrightarrow\quad c_c = 2\sqrt{m\,k}.   したがって “2√(m k)” は、「ちょうど臨界減衰になるときのダンパ係数」の大きさを表す式、という意味になります。

2√(m k)” は、「ちょうど臨界減衰になるときのダンパ係数なので、減衰比は1ですか？

はい、そのとおりです。 臨界減衰係数 (c_c = 2\sqrt{m k}) のとき、減衰比は [ \zeta = \frac{c}{2\sqrt{m k}} = \frac{c_c}{2\sqrt{m k}} = 1 ] となります。

✅ 意味の整理

項目 記号 条件 系の状態
不足減衰 (\zeta < 1) (c < c_c) 振動しながら減衰（オーバーシュートあり）
臨界減衰 (\zeta = 1) (c = c_c = 2\sqrt{m k}) 最も早く無振動で静止
過減衰 (\zeta > 1) (c > c_c) 振動せずゆっくり戻る（遅い）

💡 物理的な意味

  • 減衰比が 1（臨界減衰） のとき、システムは振動せずに最短時間で平衡位置に戻る。
  • 減衰がそれより小さいと（ζ<1）振動を伴う。
  • 減衰が大きすぎると（ζ>1）振動しないが時間がかかる。
したがって、
「(c = 2\sqrt{m k}) のとき減衰比は1ですか？」 → はい、減衰比は1で、これを臨界減衰状態といいます。

ダンパの減衰係数cと系全体の減衰係数が一致しているときに、もっとも早く静止するのですか？

とても良い質問です。 ここでポイントは，「ダンパの減衰係数 (c)」と「系全体の減衰特性」の関係を明確に区別することです。

🧩 基本：運動方程式

1自由度系 [ m\ddot{x} + c\dot{x} + kx = 0 ] では，減衰係数 (c) は「ダンパの粘性係数（比例定数）」そのものです。 系全体の減衰比は [ \zeta = \frac{c}{2\sqrt{mk}} ] で定義され，臨界減衰時（最も早く静止）には [ c = c_c = 2\sqrt{mk} \quad\Rightarrow\quad \zeta = 1 ]

⚙️ つまり：

  • ダンパの減衰係数 (c) が 系の臨界減衰係数 (c_c) に一致したとき（つまり (\zeta=1) のとき） → 最も速く静止（オーバーシュートなしで元の位置に戻る）
  • (c < c_c)（不足減衰）では振動を伴って徐々に静止
  • (c > c_c)（過減衰）では振動しないが、逆にゆっくり静止（遅くなる）

📊 イメージで言うと

減衰状態 ダンパ係数 (c) 重心の動き 静止までの時間
不足減衰 ((\zeta<1)) 小さい 振動を伴いながら収束 中くらい（振動分で余計に時間）
臨界減衰 ((\zeta=1)) ちょうど良い (c=c_c) 振動なしで一番速く収束 最短
過減衰 ((\zeta>1)) 大きい 振動せずゆっくり戻る 遅い

💡 直感的な理解

  • ダンパが弱い → 減衰不足 → 何度も振り返して時間がかかる
  • ダンパが強すぎ → 動きにブレーキがかかりすぎてゆっくりしか戻らない
  • ちょうど臨界減衰（(c=c_c)） → 最速で止まる

✅ 結論

「ダンパの減衰係数 (c) と系の臨界減衰係数 (c_c=2\sqrt{mk}) が一致するとき、最も早く静止する」 → はい、正解です。 その状態が「臨界減衰（critical damping）」であり、減衰比 (\zeta = 1) です。
 

減衰係数はなぜ重根が0となるのですか？

とても鋭い質問です。 「減衰係数が臨界値 (c = c_c = 2\sqrt{mk}) のときに“重根になる”」というのは、運動方程式の特性方程式がちょうど重解（判別式=0）を持つことを意味します。 以下でその理由を数式で説明します。

1. 基本方程式

自由振動（外力なし）： [ m\ddot{x} + c\dot{x} + kx = 0 ] これをラプラス変換や指数解 (x=e^{st}) を仮定して代入すると、特性方程式は： [ m s^2 + c s + k = 0 ]

2. 判別式（根の種類を決める）

二次方程式 [ m s^2 + c s + k = 0 ] の判別式 (D) は [ D = c^2 - 4mk ] これによって根の性質が変わります。
状態 判別式 (D=c^2-4mk) 根の形 減衰状態
(D>0) (c^2 > 4mk) 実数・異なる2根 過減衰
(D=0) (c^2 = 4mk) 実数・重根 臨界減衰
(D<0) (c^2 < 4mk) 複素共役根 不足減衰

3. 「重根が0になる」＝「判別式が0」

つまり、 [ D = c^2 - 4mk = 0 ] のとき、 [ c = 2\sqrt{mk} = c_c ] このときの根は [ s = -\frac{c}{2m} = -\frac{c_c}{2m} = -\sqrt{\frac{k}{m}} = -\omega_n ] という重根になります。

4. 物理的な意味

  • (D<0)：減衰が小さい → 複素根 → 振動（不足減衰）
  • (D>0)：減衰が大きい → 実根2つ → 振動せず遅い収束（過減衰）
  • (D=0)：ちょうど臨界 → 実根が重なり (s=-\omega_n) → 振動せず最速で収束
つまり、「判別式が0になる＝根が重なる＝臨界減衰」なのです。

✅ まとめ

項目 数式 意味
特性方程式 (m s^2 + c s + k = 0) 減衰付き振動の運動方程式
判別式 (D = c^2 - 4mk) 根の種類を決める値
臨界条件 (D = 0) 重根発生・最速収束
臨界減衰係数 (c_c = 2\sqrt{mk}) 振動せず最速で静止する条件
🔹要するに
減衰係数が臨界値 (c = 2\sqrt{mk}) のとき、二次方程式の判別式が0になり、根が重なる（重根になる）。 これが「臨界減衰（critical damping）」の定義です。
 

なぜ系全体の減衰比は \zeta = \frac{c}{2\sqrt{mk}} と定義されているのですか？

とても良い質問です。 この式 [ \boxed{\zeta = \frac{c}{2\sqrt{m k}}} ] は「系の物理パラメータ (m,k,c) と，その系がどれくらい減衰しているか（運動エネルギーがどのくらい早く失われるか）」を無次元的に表す指標です。 なぜこの形になるのかを、物理と数学の両面から説明します。

🧩 1. 運動方程式からの導出

ばね‐質量‐ダンパ系： [ m\ddot{x} + c\dot{x} + kx = 0 ] 全ての項を (m) で割ると： [ \ddot{x} + \frac{c}{m}\dot{x} + \frac{k}{m}x = 0 ] ここで [ \omega_n = \sqrt{\frac{k}{m}} \quad \text{（固有角振動数）} ] を導入して書き直すと， [ \ddot{x} + \frac{c}{m}\dot{x} + \omega_n^2 x = 0 ]

⚙️ 2. 標準形への変形

次のように係数を「無次元化」しておくと便利です： [ \ddot{x} + 2\zeta \omega_n \dot{x} + \omega_n^2 x = 0 ] この形にそろえると、系の性質を ζ という1つの無次元数で比較できるようになります。 2つの式を比べると、 [ \frac{c}{m} = 2\zeta\omega_n \quad\Rightarrow\quad \boxed{\zeta = \frac{c}{2m\omega_n} = \frac{c}{2\sqrt{mk}}}. ]

⚖️ 3. なぜこの形が「自然」なのか（物理的意味）

  • 分子 (c)：粘性減衰の強さ（単位 N·s/m）＝速度に比例する抵抗の強さ
  • 分母 (2\sqrt{m k})：臨界減衰係数 (c_c)
    • 「振動せずに最短時間で静止する」条件から導かれる値（判別式=0の条件）
    • (c_c=2\sqrt{m k})
したがって、 [ \zeta = \frac{c}{c_c} ] となり、「臨界減衰に対してどの程度の割合で減衰しているか」を表す無次元比になります。

📊 4. ζ の意味と分類

減衰比 ζ 系の状態 応答の特徴
ζ = 0 無減衰 振動が止まらない
0 < ζ < 1 不足減衰 振動しながら収束
ζ = 1 臨界減衰 振動せず最短で静止
ζ > 1 過減衰 振動せずゆっくり静止

🧠 5. まとめ（なぜこの形にしたか）

  • 方程式を「標準形」に整理すると自然にこの形が出てくる。
  • (2\sqrt{mk}) は臨界減衰係数 → 比率で表すと無次元化できる。
  • 無次元化された (\zeta) によって、異なる系でも「どれだけ減衰しているか」を同じ基準で比較できる。
🔹結論：
減衰比 (\zeta = \dfrac{c}{2\sqrt{mk}}) は、 「実際の減衰係数 (c) が臨界減衰係数 (c_c = 2\sqrt{mk}) に対してどの程度の割合か」 を表す無次元量として、運動方程式を標準化したときに自然に現れるため、この形で定義されています。