令和3年度技術士第一次試験問題［機械部門］　専門科目Ⅲ-19　ばねと定滑車とおもりからなる系の固有周期

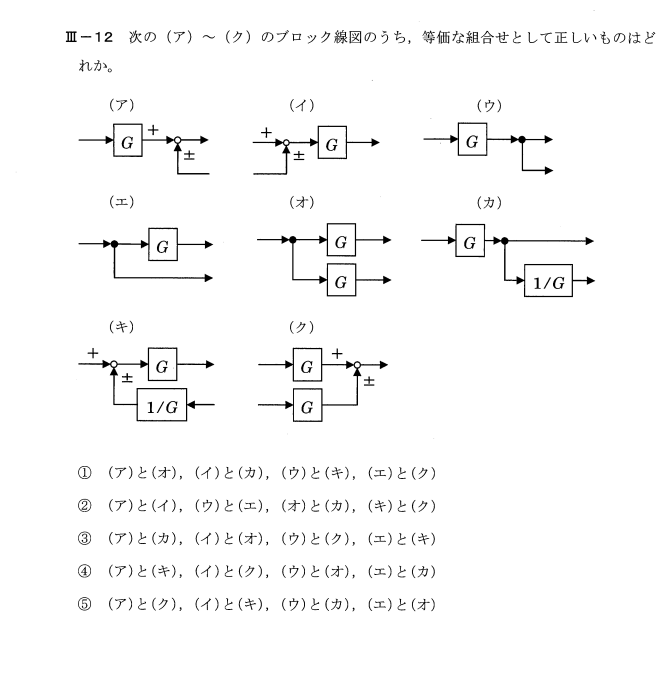
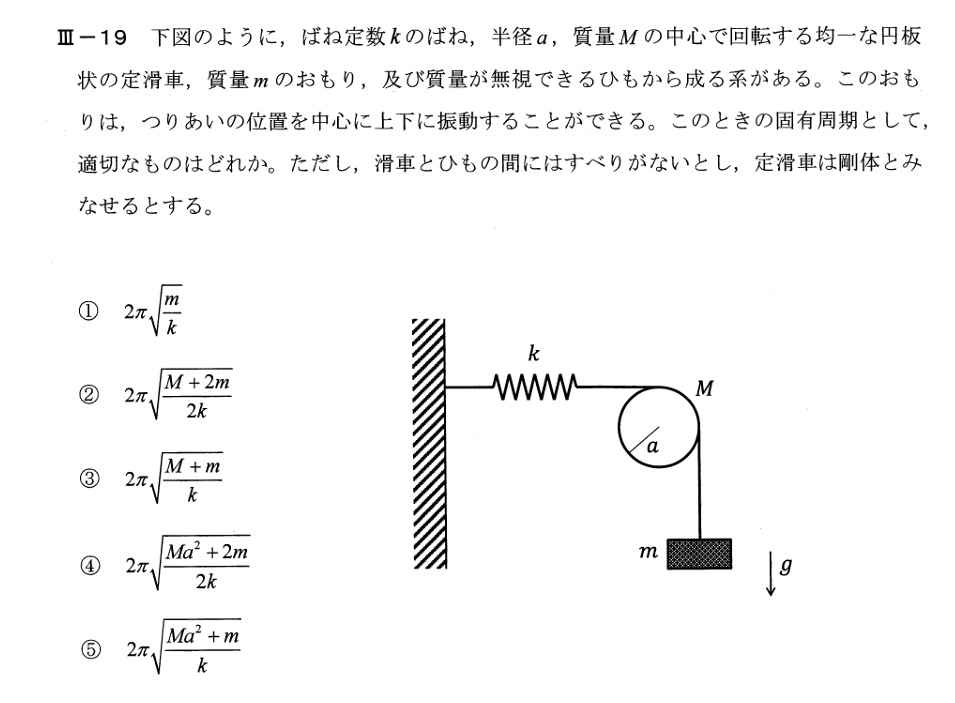
ひもの張力をFとするとおもりの運動方程式は
$$m\frac{d^2x}{dt^2} = mg – F$$

定滑車の回転に関する運動方程式は回転角をθ慣性モーメントをIとすると
$$I\frac{d^2θ}{dt^2} = (F – kx)a = Fa – kax$$

$$F =  \frac{I}{a}\frac{d^2θ}{dt^2} + kx$$

$$m\frac{d^2x}{dt^2} = mg – \frac{I}{a}\frac{d^2θ}{dt^2}  – kx$$

$x = aθ$ より

$$m\frac{d^2x}{dt^2} = mg – \frac{I}{a^2}\frac{d^2x}{dt^2}  – kx$$

$$(m + \frac{I}{a^2})\frac{d^2x}{dt^2} + kx = mg$$

$I = \frac{1}{2}Ma^2$より

$$(m + \frac{1}{2}M)\frac{d^2x}{dt^2} + kx = mg$$

$$ω_n = \sqrt{\frac{k}{m + \frac{1}{2}M}} = \sqrt{\frac{2k}{2m + M}}$$

$$ω_n = 2πf = \frac{2π}{T}$$

$$T =  2π\sqrt{\frac{Ｍ +2ｍ}{2k}}$$

[解答]②

参考

回転軸まわりの慣性モーメントと固有角振動数（H26）

回転体の慣性モーメント（H25）