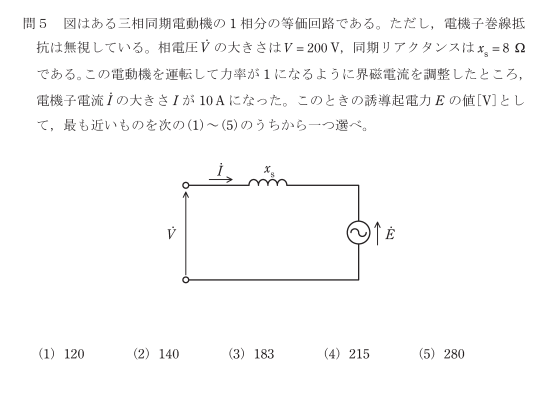
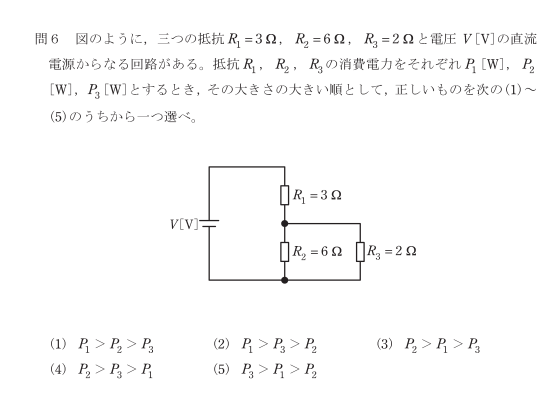
 $R_2$、$R_3$の合成抵抗は
$\frac{ 1 }{R}= \frac{ 1 }{6}+\frac{ 1 }{2}=\frac{ 2 }{3}$
$R= \frac{ 3 }{2}$
$R_1$、$R_2$、$R_3$にかかる電圧は、
$\frac{ 2 }{3}V$、$\frac{ 1 }{3}V$、$\frac{ 1 }{3}V$
となるので、消費電力は
$P_1= \frac{ V^2 }{R}=\frac{ 2^2 }{3^3}≒0.148V^2$
$P_2= \frac{ 1 }{6×3^2}≒0.0185V^2$
$P_3= \frac{ 1 }{2×3^2}≒0.0554V^2$
となり,大きい順に並べると, P1>P3>P2 と求められる。
[解答②]
<参考>
【おすすめテキスト】
$R_2$、$R_3$の合成抵抗は
$\frac{ 1 }{R}= \frac{ 1 }{6}+\frac{ 1 }{2}=\frac{ 2 }{3}$
$R= \frac{ 3 }{2}$
$R_1$、$R_2$、$R_3$にかかる電圧は、
$\frac{ 2 }{3}V$、$\frac{ 1 }{3}V$、$\frac{ 1 }{3}V$
となるので、消費電力は
$P_1= \frac{ V^2 }{R}=\frac{ 2^2 }{3^3}≒0.148V^2$
$P_2= \frac{ 1 }{6×3^2}≒0.0185V^2$
$P_3= \frac{ 1 }{2×3^2}≒0.0554V^2$
となり,大きい順に並べると, P1>P3>P2 と求められる。
[解答②]
<参考>
【おすすめテキスト】
【電験3種(R2年度)】理論科目:問6 抵抗で消費される電力に関する計算問題
- 更新日:
- 公開日:
 $R_2$、$R_3$の合成抵抗は
$\frac{ 1 }{R}= \frac{ 1 }{6}+\frac{ 1 }{2}=\frac{ 2 }{3}$
$R= \frac{ 3 }{2}$
$R_1$、$R_2$、$R_3$にかかる電圧は、
$\frac{ 2 }{3}V$、$\frac{ 1 }{3}V$、$\frac{ 1 }{3}V$
となるので、消費電力は
$P_1= \frac{ V^2 }{R}=\frac{ 2^2 }{3^3}≒0.148V^2$
$P_2= \frac{ 1 }{6×3^2}≒0.0185V^2$
$P_3= \frac{ 1 }{2×3^2}≒0.0554V^2$
となり,大きい順に並べると, P1>P3>P2 と求められる。
[解答②]
<参考>
【おすすめテキスト】
$R_2$、$R_3$の合成抵抗は
$\frac{ 1 }{R}= \frac{ 1 }{6}+\frac{ 1 }{2}=\frac{ 2 }{3}$
$R= \frac{ 3 }{2}$
$R_1$、$R_2$、$R_3$にかかる電圧は、
$\frac{ 2 }{3}V$、$\frac{ 1 }{3}V$、$\frac{ 1 }{3}V$
となるので、消費電力は
$P_1= \frac{ V^2 }{R}=\frac{ 2^2 }{3^3}≒0.148V^2$
$P_2= \frac{ 1 }{6×3^2}≒0.0185V^2$
$P_3= \frac{ 1 }{2×3^2}≒0.0554V^2$
となり,大きい順に並べると, P1>P3>P2 と求められる。
[解答②]
<参考>
【おすすめテキスト】