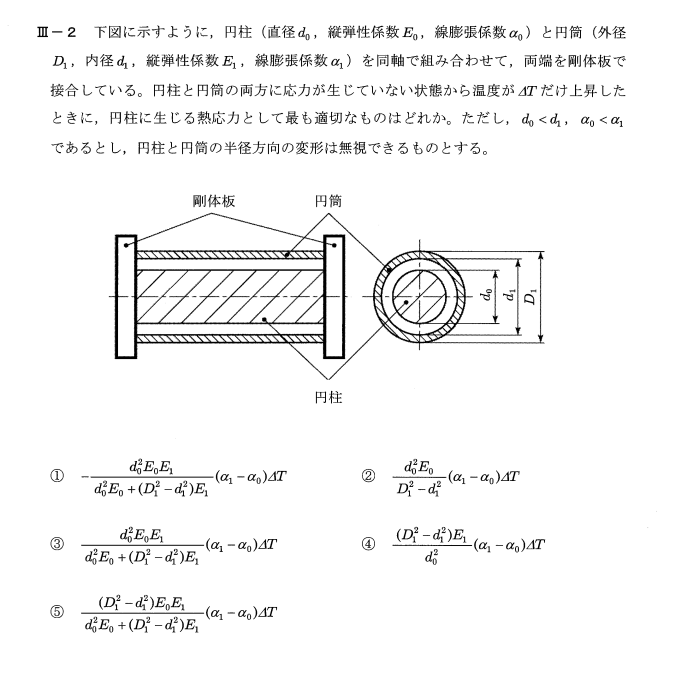
 温度がΔTだけ上昇した時の円柱にかかる熱応力を$σ_0$とすると、ひずみ$ε_0$は、熱による膨張分と剛体板から受ける力の和となり
$ ε_0 = α_0ΔT + \frac{ σ_0 }{ E_0 }$
同様に、温度がΔTだけ上昇した時の円筒にかかる熱応力を$σ_1$とすると、ひずみ$ε_1$は、熱による膨張分と剛体板から受ける力の和となり
$ ε_1 = α_1ΔT + \frac{ σ_1 }{ E_1 }$
ここで、円柱と円筒は剛体板で接続されているので、$ε_0 = ε_1$ となり、
$ α_0ΔT + \frac{ σ_0 }{ E_0 } = α_1ΔT + \frac{ σ_1 }{ E_1 }$
$ σ_1 = -E(α_1 - α_0)ΔT + \frac{ E_1 }{ E_0 }σ_0$ ・・・①
次に、ちからのつり合いから、円柱と円筒の両方に発生する軸力は等しいので、円柱の断面積を$A_0$、円筒の断面席を$A_1$として
$A_0σ_0 +A_1σ_1 = 0 $
$\frac{ d_0^2 }{ 4 }πσ_0 + \frac{ D_1^2 - d_1^2}{ 4 }πσ_1 = 0$・・・②
①、②より
$σ_0 = \frac{ (D_1^2 - d_1^2)E_0E_1 }{ d_0^2E_0+(D_1^2 - d_1^2)E_1 }(α_1 - α_0)ΔT$
[解答] ⑤
温度がΔTだけ上昇した時の円柱にかかる熱応力を$σ_0$とすると、ひずみ$ε_0$は、熱による膨張分と剛体板から受ける力の和となり
$ ε_0 = α_0ΔT + \frac{ σ_0 }{ E_0 }$
同様に、温度がΔTだけ上昇した時の円筒にかかる熱応力を$σ_1$とすると、ひずみ$ε_1$は、熱による膨張分と剛体板から受ける力の和となり
$ ε_1 = α_1ΔT + \frac{ σ_1 }{ E_1 }$
ここで、円柱と円筒は剛体板で接続されているので、$ε_0 = ε_1$ となり、
$ α_0ΔT + \frac{ σ_0 }{ E_0 } = α_1ΔT + \frac{ σ_1 }{ E_1 }$
$ σ_1 = -E(α_1 - α_0)ΔT + \frac{ E_1 }{ E_0 }σ_0$ ・・・①
次に、ちからのつり合いから、円柱と円筒の両方に発生する軸力は等しいので、円柱の断面積を$A_0$、円筒の断面席を$A_1$として
$A_0σ_0 +A_1σ_1 = 0 $
$\frac{ d_0^2 }{ 4 }πσ_0 + \frac{ D_1^2 - d_1^2}{ 4 }πσ_1 = 0$・・・②
①、②より
$σ_0 = \frac{ (D_1^2 - d_1^2)E_0E_1 }{ d_0^2E_0+(D_1^2 - d_1^2)E_1 }(α_1 - α_0)ΔT$
[解答] ⑤
ポイント
・円筒、円柱の変形量は熱応力と、剛体板から受ける(圧縮、引張)応力の和になる。
・円筒、円柱の変形量と軸力は等しくなる。
参考:【材料力学】熱応力の不静定問題を初心者でも解けるよう丁寧に解説!





