フーリエ解析とは
フーリエ解析とは、周期的な信号を複数の正弦波や余弦波の和の形に分解する数学的手法です。この手法は、周期的な信号の周波数成分を分析し、波形や周波数スペクトルを可視化するために使用されます。具体的には、フーリエ解析は、信号を時間領域から周波数領域に変換することによって、周波数成分を分析します。この変換によって、信号がどの周波数成分から構成されているかを可視化することができます。
また、フーリエ解析は、音声、画像、ビデオなどの信号処理アプリケーションに広く使用されています。例えば、音声の場合、フーリエ解析は、音楽や話し声の周波数成分を分析し、それをスペクトル表示することができます。また、画像の場合、フーリエ解析は、画像の周波数成分を分析して、フィルタリングや圧縮などの画像処理技術に応用されます。
どのように使われているのか
フーリエ解析は、様々な分野で幅広く利用されています。以下に、フーリエ解析の主な利用例をいくつか挙げます。
音声処理：フーリエ解析は、音声信号を周波数成分に分解して、スペクトル解析を行うことができます。これにより、音声の周波数特性を分析し、音声信号に含まれるノイズを除去することができます。また、音声の圧縮やエフェクト処理にも応用されます。
映像処理：フーリエ解析は、画像を周波数成分に分解して、フィルタリングやエフェクト処理を行うことができます。また、画像圧縮技術にも応用されます。
信号解析：フーリエ解析は、電気信号や電磁波などの信号を周波数成分に分解して、スペクトル解析を行うことができます。これにより、信号の周波数特性を分析し、ノイズの除去やフィルタリングを行うことができます。
構造解析：フーリエ解析は、物体の振動を周波数成分に分解して、構造解析を行うことができます。これにより、物体の特性や強度を分析することができます。
金融分析：フーリエ解析は、金融市場の変動を周波数成分に分解して、分析することができます。これにより、市場の特性や動向を分析し、投資戦略を立てることができます。
これらのように、フーリエ解析は、多岐にわたる分野で利用されています。
金融分析において、フーリエ解析は、時系列データを周波数成分に分解して、市場の周期性や動向を分析するために使用されます。例えば、株価の時系列データをフーリエ解析することで、どのような周波数成分が含まれているかを分析することができます。これにより、市場にはどのような周期性があるかを分析し、投資戦略を立てることができます。また、市場の変動がどのような周期性を持っているかを分析することで、将来の市場の動向を予測することができます。さらに、フーリエ解析は、金融データのフィルタリングにも使用されます。例えば、時系列データからノイズを取り除くために、特定の周波数成分をカットオフすることができます。また、フーリエ解析は、オプションプライシングモデルの一部としても使用されます。オプションプライシングモデルは、株式市場の動向を予測するためのモデルであり、フーリエ解析を用いて市場の波動性をモデル化することができます。これらのように、金融分析においてフーリエ解析は、市場の動向や投資戦略の決定、金融商品のプライシングなど、様々な分野で活用されています。
数学の準備体操
三角関数
加法定理
三角関数の加法定理とは、2つの三角関数の和（または差）を、1つの三角関数やその積の形に変形する公式です。
1. **正弦の加法定理**
\[
\sin(a \pm b) = \sin a \cos b \pm \cos a \sin b
\]
2. **余弦の加法定理**
\[
\cos(a \pm b) = \cos a \cos b \mp \sin a \sin b
\]
3. **正接の加法定理**
\[
\tan(a \pm b) = \frac{\tan a \pm \tan b}{1 \mp \tan a \tan b}
\]
### 積を和に変換する公式（積和公式）
加法定理を基に、積を和に変換する公式は以下のように求められます。
1. **\(\sin a \cos b\) の積和公式**
\[
\sin a \cos b = \frac{1}{2} \left[ \sin(a + b) + \sin(a – b) \right]
\]
2. **\(\cos a \cos b\) の積和公式**
\[
\cos a \cos b = \frac{1}{2} \left[ \cos(a + b) + \cos(a – b) \right]
\]
3. **\(\sin a \sin b\) の積和公式**
\[
\sin a \sin b = \frac{1}{2} \left[ \cos(a – b) – \cos(a + b) \right]
\]
複素数
複素数は、実数と虚数の和で表される数です。虚数単位 i を用いて、a + bi と表されます。ここで、a は実数部、b は虚数部と呼ばれます。
複素数の演算は、加算、減算、乗算、除算が可能です。加算、減算は実数の場合と同じように行います。乗算は、実数の乗算に加えて、虚数同士の乗算や、虚数と実数の乗算においても、以下の公式を用いることができます。
(i^2 = -1)
(a+bi)(c+di) = (ac – bd) + (ad + bc)i
また、除算は、分母と分子に共役複素数をかけることで、以下の公式を用いることができます。
(a+bi) / (c+di) = (a+bi)(c-di) / (c^2 + d^2)
複素数には、モジュラスと偏角という概念があります。モジュラスは、複素数の絶対値を表し、以下の公式で求めることができます。
|a+bi| = sqrt(a^2 + b^2)
偏角は、複素数の極座標形式で表される角度を表し、以下の公式で求めることができます。
θ = tan^(-1)(b / a)
これらの基本的な知識を理解していると、複素数を用いたフーリエ解析や信号処理の理解が容易になります。
オイラーの公式
オイラーの公式は、以下のように表されます。
e^(ix) = cos(x) + i*sin(x)
ここで、e はネイピア数（自然対数の底）、i は虚数単位、x は実数です。この公式は、三角関数（sin, cos）と指数関数（e^(x)）との関係を示しており、数学や物理学の分野で広く利用されています。
この公式は、指数関数のマクローリン級数展開を用いることで導出することができます。指数関数のマクローリン級数展開は以下のようになります。
e^(x) = 1 + x/1! + x^2/2! + x^3/3! + …
ここで、x = ix を代入すると、
e^(ix) = 1 + ix/1! + (ix)^2/2! + (ix)^3/3! + …
= 1 + ix – x^2/2! – ix^3/3! + …
= (1 – x^2/2! + x^4/4! – …) + i(x – x^3/3! + x^5/5! – …)
= cos(x) + i*sin(x)
となり、オイラーの公式が導かれます。
フーリエ解析では、周期的な信号を複数の正弦波（sin関数）や余弦波（cos関数）の重ね合わせに分解することができます。この際に、オイラーの公式を用いることで、正弦波と余弦波を複素指数関数の形で表現することができます。
具体的には、周期 T を持つ信号 f(t) をフーリエ級数展開する際に、以下の式が用いられます。
f(t) = a_0 + Σ(n=1 to ∞) [a_ncos(2πnTt/T) + b_nsin(2πnTt/T)]
ここで、a_n と b_n はフーリエ係数と呼ばれる定数で、f(t) の周期的な性質を表す重要なパラメーターです。これらの係数を求めるために、オイラーの公式を使って、sin関数とcos関数を複素指数関数の形に変換することができます。具体的には、以下の式を用いて、cos関数とsin関数を複素指数関数に変換することができます。
cos(x) = (e^(ix) + e^(-ix))/2
sin(x) = (e^(ix) – e^(-ix))/(2i)
このようにして、複素指数関数を用いることで、フーリエ級数展開をより簡単に扱うことができます。
直交関数列
数学において直交関数列（ちょっこうかんすうれつ、英: orthogonal functions）とは互いに直交する関数列の事である。
区間 (α, β) (−∞ ≤ α < β ≤ ∞) 上で定義された複素数値関数 f(x), g(x) に対し
は、積分が有限値として存在するならば、内積となる。
(α, β) 上の複素値関数の列 {φn(x)} が、この内積に対し、互いに直交し、
であるとき、直交関数列であるという。
特に直交関数列のうち、ノルムが 1、すなわち
であるものものを正規直交関数列という。
また、実数値関数の列 {φn(x )} とある関数 w(x) ≥ 0 に対し、{(w(x))1/2φn(x)} が直交関数列をなし、
であるとき、この関数列を重み（荷重）w(x) の直交関数列という。
参考：https://ja.wikipedia.org/wiki/%E7%9B%B4%E4%BA%A4%E9%96%A2%E6%95%B0%E5%88%97
フーリエ級数展開
関数 \( f(t) \) が周期 \( 2\pi \) の場合、フーリエ級数は次のようになります：
\[
f(t) = a_0 + \sum_{n=1}^{\infty} \left[ a_n \cos(n t) + b_n \sin(n t) \right]
\]
係数は：
\[
a_0 = \frac{1}{2\pi} \int_{-\pi}^{\pi} f(t) \, dt
\]
\[
a_n = \frac{1}{\pi} \int_{-\pi}^{\pi} f(t) \cos(n t) \, dt
\]
\[
b_n = \frac{1}{\pi} \int_{-\pi}^{\pi} f(t) \sin(n t) \, dt
\]
参考：https://www2-kawakami.ct.osakafu-u.ac.jp/omu-content/uploads/sites/1161/Lecture_Data/Electric_Circuit_II/01_Lecture/26_lecture_electric_circuit_II.pdf
周期が2πでない場合
フーリエ級数は、周期的な関数を三角関数の和で表現する方法です。周期がTの関数f(t)について、フーリエ級数展開すると以下のようになります。
f(t) = a0 + Σ [an cos(nωt) + bn sin(nωt)]
ここで、ω=2π/Tは角周波数であり、a0, an, bnはフーリエ係数と呼ばれます。a0は直流成分、anとbnはそれぞれcosine成分とsine成分を表します。
周期Tの関数f(t)のフーリエ係数anとbnは以下のように求められます。
an = (2/T) ∫[0,T] f(t) cos(nωt) dt
bn = (2/T) ∫[0,T] f(t) sin(nωt) dt
ここで、ω=2π/Tは角周波数です。また、f(t)は周期Tの関数であり、∫[0,T]は0からTまでの積分を表します。anはcosine成分、bnはsine成分を表します。a0は直流成分で、a0 = (1/T) ∫[0,T] f(t) dt で求められます。
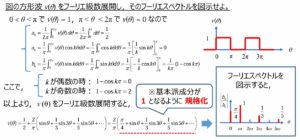
フーリエ級数展開によって、周期的な関数を三角関数の和で表現することができます。ひとつ実例を見てみましょう。
引用：東北大学 工学部 材料科学総合学科 工業数学II（小原） ２．フーリエ級数展開
不連続点におけるフーリエ級数の値は収束しないため、その値を持ちません。不連続点におけるフーリエ級数の値は、その点の左右で異なる関数値の平均になります。例えば、x=0での不連続点では、f(0-)=-1、f(0+)=1なので、その平均は0になります。
フーリエ係数についてもっと詳しく学びたい方には
慶應大学講義 物理情報数学C 第五回 フーリエ級数
フーリエ係数の公式を導出
直交性の公式は以下のようになります。
∫_a^b sin(nπx/L) sin(mπx/L) dx = {0 (n ≠ m), L/2 (n = m = 0)}
∫_a^b cos(nπx/L) cos(mπx/L) dx = {0 (n ≠ m), L/2 (n = m ≠ 0)}
∫_a^b sin(nπx/L) cos(mπx/L) dx = 0
ここで、aとbは区間の端点、Lは区間の長さ、nとmは整数です。
これを使うことでフーリエ係数を導出することができます。
詳しくは動画を確認してください。
【大学数学】フーリエ解析入門②(フーリエ級数展開 II)/全5講【解析学】
複素フーリエ級数
複素フーリエ級数は、周期関数を複素数の和として表す方法の一つで、実フーリエ級数と同様に周期関数を三角関数や正弦波の和として表すフーリエ級数展開に代わる方法です。実フーリエ級数が、三角関数の余弦と正弦の和で表現されるのに対し、複素フーリエ級数では、複素指数関数の和で表現されます。
具体的には、周期Tの関数f(x)を以下のように表現します。
f(x) = ∑_{n=-∞}^∞ c_n e^{i nω x}
ここで、ω=2π/Tは角周波数であり、c_nは複素係数であり、以下のように与えられます。
c_n = (1/T) ∫_{-T/2}^{T/2} f(x) e^{-i nω x} dx
このように、複素フーリエ級数では、実フーリエ級数のcosとsinの和を、複素数の指数関数の和で表現することができます。
複素フーリエ級数展開において、係数$c_n$は以下のようにフーリエ級数展開の係数$a_n$と$b_n$と関係しています。
$c_n = \frac{1}{2}(a_n – ib_n)$
また、逆に$a_n$と$b_n$を$c_n$で表すと以下のようになります。
$a_n = c_n + c_{-n}^*$
$b_n = \frac{1}{i}(c_n – c_{-n}^*)$
ここで、$^*$は複素共役を表します。つまり、複素フーリエ級数展開における$c_n$は、実数の$a_n$と$b_n$を含むように定義されています。
例題：
フーリエ変換
フーリエ変換は、時間領域の連続信号を周波数領域に変換する手法です。時間領域の信号を周波数成分のスペクトルに変換することで、信号の周波数特性を分析することができます。
具体的には、連続時間領域の信号f(t)をフーリエ変換F(ω)に変換することを考えます。ここでωは角周波数であり、単位はrad/sです。フーリエ変換F(ω)は以下の式で表されます。
F(ω) = ∫[ -∞ , ∞ ] f(t) e^{-iωt} dt
ここで、e^{-jωt}は複素指数関数であり、jは虚数単位です。フーリエ変換は、この式で表される積分を計算することで求めることができます。
フーリエ変換は、時間領域の信号を周波数領域に変換するため、周波数領域での信号の特性を分析することができます。具体的には、周波数領域でのスペクトルのピークや帯域幅などを分析することができます。また、逆フーリエ変換を用いることで、周波数領域で変換された信号を時間領域に戻すことができます。
逆フーリエ変換の公式は以下のように表されます。
f(t) = (1/2π) ∫[ -∞ , ∞ ] F(ω) e^(iωt) dω
ここで、F(ω)は信号の周波数スペクトル、f(t)は信号の時間軸上の波形を表します。逆フーリエ変換は、周波数スペクトルF(ω)から元の信号f(t)を再構成するために使用されます。具体的には、F(ω)を逆フーリエ変換の公式に代入し、tについて積分することで、f(t)を求めることができます。
ここで今までの復習を兼ねて、複素フーリエ級数展開とフーリエ積分公式を見てみましょう。
複素フーリエ級数展開： f(x) = ∑_{n=-∞}^{∞} c_n e^{i n ω_0 x}
フーリエ係数： c_n = 1/T ∫_{-T/2}^{T/2} f(x) e^{-i n ω_0 x} dx
ここで、ω_0 = 2π/Tは基本角周波数である。一方、非周期関数g(x)に対して、周波数領域での表現を以下のように与えることができる。
フーリエ積分公式： f(x) = (1/2π)∫_{-∞}^{∞} F(ω) e^{i ω x} dω
周波数スペクトル： F(ω) =∫_{-∞}^{∞} f(t) e^{-i ω t} dt ・・・ (フーリエ変換)
対応関係をもっと詳しく知りたい方：フーリエ積分・フーリエ変換
ラプラス変換
ラプラス変換は、時間領域の関数を複素平面上の関数に変換する操作です。具体的には、ラプラス変換を用いることで、微分方程式や積分方程式などの線型常微分方程式を解析的に解くことができます。
時間領域の関数f(t)のラプラス変換F(s)は以下の式で表されます。
F(s) = ∫[0,∞) f(t) e^(-st) dt
ここで、sは複素数のパラメーターであり、e^(-st)は複素指数関数です。
ラプラス変換は、フーリエ変換と似たような変換であり、周波数領域ではなくs領域で表されます。ラプラス変換がフーリエ変換の一般化として扱われることがあります。具体的には、ラプラス変換は、フーリエ変換をs軸に沿って解析接続したものとして表現されることがあります。また、特定の条件が満たされる場合には、ラプラス変換とフーリエ変換は一致することがあります。
ただし、ラプラス変換とフーリエ変換は、変換の対象となる関数が異なるため、適用する問題や場面が異なることがあります。ラプラス変換は、時刻0から無限遠に向かって発生する信号や、初期値が与えられた微分方程式の解析に適しています。一方、フーリエ変換は、周期的な信号や、周波数成分を抽出したい信号の解析に適しています。
ラプラス変換表
ラプラス変換表は、与えられた関数をラプラス変換する際に、どのようなラプラス変換公式を使用すればよいかを示す参考書として使用されます。
| 時間領域関数 f(t) | ラプラス領域関数 F(s) |
| 単位ステップ関数 u(t) | 1/s |
| tn (n >= 0) | n!/s^(n+1) |
| e^-at | 1/(s+a) |
| cos(wt) | s/(s^2+w^2) |
| sin(wt) | w/(s^2+w^2) |
| e^-at cos(wt) | (s+a)/( (s+a)^2 + w^2 ) |
| e^-at sin(wt) | w/( (s+a)^2 + w^2 ) |
| t^n e^-at | n!/ (s+a)^(n+1) |
| δ(t) | 1 |
| δ(t-a) | e^-as |
| f(t) + g(t) | F(s) + G(s) |
| kf(t) | kF(s) |
| f(t-a) u(t-a) | e^-as F(s) |
| ∫f(t)dt (積分区間0からt) | F(s)/s |
| df(t)/dt | sF(s) – f(0) |
| ∫f(t)e^-stdt | F(s + iω) |
| f'(t) | sF(s) – f(0) |
| f”(t) | s^2 F(s) – sf(0) – f'(0) |
離散フーリエ変換
離散フーリエ変換（Discrete Fourier Transform, DFT）は、離散的な信号を周波数領域で表現する手法のひとつで、ディジタル信号処理において広く使われています。DFTは、有限個のサンプルを等間隔に取得したディジタル信号を、そのサンプルが表す周期関数の周波数成分を表す複素数値の列として表現します。
DFTにおいては、離散的なサンプルの数によって周波数分解能が決まります。具体的には、N個のサンプルを等間隔に取得した場合、周波数領域では0から(N-1)の整数に対応する周波数成分を表現することができます。また、DFTの逆変換によって、周波数領域で表現された信号を元の時間領域の信号に戻すことができます。
一般的なフーリエ変換は連続時間信号を周波数領域に変換するものであり、積分が使われます。一方、離散フーリエ変換は、離散時間信号を周波数領域に変換するものであり、和が使われます。和が用いられるのは周波数領域での信号の振幅と位相は、サンプリング周波数の整数倍の周波数の成分のみで決まり、それ以外の周波数成分では0となるからです。つまり積分型のフーリエ変換をすると結果が0になります。
フーリエ変換の公式
時系列関数 f(t) に対して、フーリエ変換 F(ω) は以下のように定義される。
F(ω) = ∫︎_{-∞}^∞ f(t) e^{-iωt} dt
離散フーリエ変換の公式
離散的な時系列関数 x[n] に対して、離散フーリエ変換 X[k] は以下のように定義される。
X[k] = ∑_{n=0}^{N-1} x[n] e^{-i(2π/N)kn}
ここで、N は x[n] のサンプル数である。
詳しくはこちら：離散フーリエ変換(DFT)の仕組みを完全に理解する
最後に・・・
フーリエ解析，ラプラス変換，線形システム論，制御論などもっと理解を深めたい方はこちらに進んでください。
詳しくはこちら：離散フーリエ変換(DFT)の仕組みを完全に理解する
信号処理とは
信号処理はどんなときに必要か
信号処理は、さまざまな分野で必要とされ、特に以下のような状況や用途で重要です
音声処理：音声の録音や通話の際、ノイズを除去したり、音質を改善したりするために信号処理が使われます。音声認識や音声合成にも応用されています。
画像処理：カメラで撮影された画像や動画のクオリティを向上させたり、画像の中から特定の情報を抽出するために必要です。例えば、顔認識や医療画像処理などで信号処理が使われます。
通信：デジタル通信や無線通信では、送信された信号がノイズや干渉によって歪むことがあるため、信号処理によってデータの復元やエラーの補正が行われます。
医療分野：心電図(ECG)や脳波(EEG)などの生体信号を解析する際、信号処理が使用されます。これにより、診断や治療に役立つ情報を得ることができます。
音楽やエンターテイメント：デジタル音楽の制作、編集、圧縮（例えばMP3形式）においても、信号処理が活用されます。音楽のエフェクト追加や音量調整も信号処理の一部です。
自動車分野：レーダーやライダーを使った自動運転技術において、センサーからの信号を処理して周囲の状況を把握し、運転に反映させるために使われます。
AIや機械学習：AIシステムが学習データを扱う際、データを前処理したり、特徴を抽出するために信号処理技術が応用されます。
実際に、機械で加工の分野でも切削音の信号から切削工具の交換時期をコンピュータに自動的に判断させるような信号技術が考案されていたりもします。信号処理は、アナログデータをデジタルデータに変換し、さらにそのデータを分析、最適化、圧縮するための手段として、多くの技術的分野で不可欠な役割を果たしています。
アナログ信号とディジタル信号
例えば気温の時間的変化を信号として観測することを考えると、気温は連続的に変化するので、その値の時間的すきまはない。しかし、測定データとして記録したときには測定を行った間隔ができてしまう。だからといって気温は1秒や1分で急激に変化することはまずありえない。したがってもっと粗い時間間隔で測定したとしても不都合はなく、データの保存容量も少なくて済む。また精度についても同様で、必要以上の桁数まで測定することは無駄になる。
- アナログ信号
アナログ信号は、連続的な変化を持つ信号で、時間の経過とともに滑らかに変化します。物理的な現象や自然界の多くのデータはアナログ信号として表現されます。
特徴：
連続性：アナログ信号は無限の値を取ることができ、信号の変化が滑らかです。例えば、音や光の強さ、温度などがアナログ信号です。
例：音声信号、温度変化、光の強弱などがアナログ信号の例です。たとえば、マイクで録音された音声は、空気中の振動を連続的に電気信号に変換したものです。
長所：滑らかで自然な信号表現が可能なため、アナログ信号は非常に正確に物理現象を表現できます。
短所：ノイズや劣化に弱い点があります。特に信号の伝送や記録の過程で、ノイズが加わりやすく、信号が劣化しやすいです。
- ディジタル信号
ディジタル信号は、離散的な値で表現される信号です。一般的に「0」と「1」の二進数で情報を表現し、信号は時間の経過に応じて飛び飛びの値を取ります。
特徴：
離散性：ディジタル信号は連続していないため、ある瞬間ごとに特定の値（多くの場合は0か1）を取ります。これにより、正確な数値として処理されます。
例：コンピュータやスマートフォンが扱うデータはすべてディジタル信号です。CDやMP3に変換された音楽、JPEG形式の画像もディジタル信号です。
長所：ディジタル信号はノイズに強く、複製や圧縮が容易です。また、エラー検出や修正が可能であり、信号の劣化が少なく済みます。
短所：デジタル信号はアナログ信号をサンプリングして離散化するため、アナログ信号ほどの連続性や自然さが失われる可能性があります。ただし、高品質なサンプリングを行えば、ほぼアナログ信号に近い表現も可能です。
| 特徴 | アナログ信号 | ディジタル信号 |
| 変化の仕方 | 連続的 | 飛び飛びの離散的な変化 |
| 情報の表現 | 連続値で表現される | 二進数（0と1）で表現される |
| ノイズ耐性 | ノイズに弱く、信号が劣化しやすい | ノイズに強く、信号が劣化しにくい |
| 例 | 音声、温度、光、電圧など | コンピュータデータ、デジタル音声、デジタル映像など |
| 応用 | アナログラジオ、レコード、アナログテレビ | デジタル通信、CD、スマートフォン、ストリーミングサービス |
アナログ信号とは、連続的に変化する信号であり、自然界に存在する多くのデータ（音声、光、温度など）はアナログ信号として表現されます。この信号は時間の経過とともに滑らかに変化し、無限の値を持つことが特徴です。しかし、アナログ信号はそのままではデジタルデバイスで直接扱えないため、**AD変換（アナログ–デジタル変換）**を通じてディジタル信号に変換する必要があります。
AD変換の第一歩は離散化です。アナログ信号は時間の連続的なデータですが、デジタル処理では飛び飛びのデータ（離散的なデータ）に変える必要があります。これを行うために、**標本化（サンプリング）**というプロセスを実行します。標本化は、アナログ信号を一定の時間間隔で測定し、その時点の信号の値を記録するものです。次に、サンプリングされたデータは連続的な値を持っていますが、デジタルデバイスで処理するためには、これを離散的な数値（ビット）で表現する必要があります。このステップを量子化と呼びます。量子化では、サンプリングされた信号の値を、一定の範囲内で最も近い数値に丸めることで、信号を有限のレベルに変換します。たとえば、16ビットの量子化では、信号を65,536段階に分けて近似します。こうして、標本化と量子化を経た信号は、最終的にディジタル信号になります。ディジタル信号は、0と1の二進数で表される信号であり、コンピュータやデジタル機器で簡単に処理、保存、伝送できます。また、ノイズや劣化に強いため、信号の品質が保たれやすいという利点があります。この一連のプロセス、すなわちアナログ信号をAD変換によってディジタル信号に変換するステップは、オーディオ、映像、通信、医療など、さまざまな分野で不可欠です。この変換によって、連続的な現実世界の情報がデジタルの形で利用可能になり、より高い精度で処理できるようになります。
同期加算
同期加算は、信号処理において重要な技術で、主にノイズの多い信号から目的の信号を抽出するために使用されます。同期加算とは、同じ信号を複数回取得し、それらを正確にタイミングを合わせて（同期して）加算する処理のことです。この手法は、信号とノイズの特性の違いを利用しています。
信号の特性: 目的の信号は、同期して加算されるため、その平均振幅は変わりません。
ノイズの特性: ノイズは通常、信号とは独立しており、ランダムな性質を持っています。そのため、加算を重ねるとノイズ同士が打ち消し合う傾向があります6。
同期加算の効果
S/N比の改善: 同期加算を行うことで、信号対ノイズ比（S/N比）が向上します。
ノイズの低減: K回の同期加算を行うと、ノイズの振幅は理論的に1/√K倍に減少します。
信号の強調: 目的の信号は加算によって強調されます。
同期加算の数学的表現は以下のようになります：
$h(n) = \frac{1}{N} \sum_{i=1}^{N} \left( s_i(n) + n_i(n) \right)$
$h(n)$ は同期加算後の信号
$N$ は加算回数
$s_i(n)$ は i 回目の目的信号
$n_i(n)$ は i 回目のノイズ成分
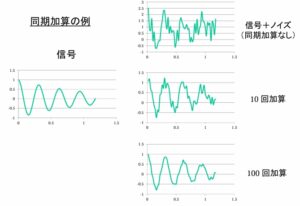
参考：https://hapislab.org/public/hiroyuki_shinoda/keisoku_joho/20_02.pdf
多数の測定値を加えていき、平均をとると、雑音の和は結局は0に近づいていく。したがって、雑音成分に乱されながらも同じ信号成分を含んだ信号波形を同期をとりながら加算していき、平均をとると、結局本来の信号成分が表れてくるのである。
