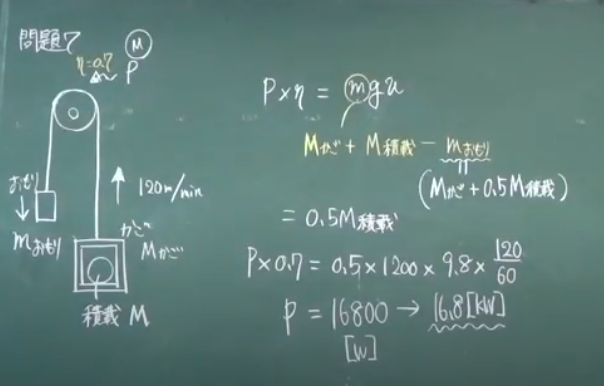【問題】(pdfファイル)

ダウンロードして使用してください。

問題と解答

問題１
１次巻線n1,２次巻線n2の変圧器を周波数f[Hz]で運転している。最大磁束φm[Wb],巻数比をaとして以下 の問いに答えよ。 (１)一次巻線および二次巻線の誘導起電力E1,E2を求めよ。

E=4.44fnΦm E1=4.44n1Φm E2=4.44n2Φm E1/E2=n1/n2=a I1/I2=V2/V1=1/a

(２)変圧器の二次側を一次側に換算した場合,以下の値はaを用いて何倍されたものに換算されるか。
  • 二次側の端子電圧V2 ②二次側の電流I2  ③二次側のインピーダンスZ2

E1=aE2 I1=1/aI2 Z1=a^2Z2

(３)変圧器の一次側を二次側に換算した場合,以下の値はaを用いて何倍されたものに換算されるか。
  • 一次側の端子電圧V1 ②一次側の電流I1  ③一次側のインピーダンスZ2

E2=1/aE1 I2=aI1 Z2=1/a^2Z1

④励磁電流I0                                  ⑤励磁アドミタンスY0

I0'=aI0 Y0'=a^2Y0

問題２
変圧器の損失について,以下の問いに答えよ。

鉄損＝ヒステリシス損+うず電流損 Pi=k1V^(1.6~2)/f+k2V2

銅損=抵抗損 Pc＝rI^2

  • 定格電圧の下で負荷を２倍にしたとき,鉄損と銅損はそれぞれどのように変化するか。

負荷２倍⇒電流2倍 鉄損：変化なし 銅損：4倍

  • 定格電圧の下で力率を１から8(遅れ)にしたとき,鉄損と銅損はそれぞれどのように変化するか。

pi,pc共に変化なし

  • 電圧を２倍にしたとき,鉄損はどのように変化するか。

ほぼ4倍になる

  • 周波数を小さくしたとき,鉄損と銅損はそれぞれどのように変化するか。

pi：大きくなる。pc:変化なし

問題３
変圧器の結線方式について,以下の①～③の文のうち,正しいものには○,誤っているものには×をつけよ。
  • ３台の変圧器を用いる際,一般的にΔ－Δ結線やＹ－Ｙ結線の結線方式を行う。

×　Y-Yは一般に用いられない

  • Ｖ－Ｖ結線の出力は,変圧器１台の √3倍であり,その利用率は86.6%である。

〇　出力√3P　利用率√3P/2P＝0.866

  • Ｖ－Ｖ結線の銅損は,Δ－Δ結線の銅損の0.67倍である。

×　V：2ｒI^2　Δ：3r(1/√3I）^2=ri^2

問題４
以下の変圧器について,下線部に適する語句をそれぞれ答えよ。
変圧器の名称 説明
①三巻線変圧器 一次,二次巻線をY-Y 結線にし,三次巻線をΔ 結線とする
②アモルファス変圧器 ケイ素鋼板に比べ, 銅損が1/3以下に減少する
③磁気漏れ変圧器 負荷時に大きい漏れ磁束が生じる。普通の変圧器よりも電圧変動率が大きい
④モールド変圧器 巻線をエポキシ樹脂(合成樹脂)で覆ったもので, 難燃性に優れている。
問題５
単相変圧器1000［kV・A］,20kV/6.6kVにおいて二次側を短絡して一次側に定格電流を流して短絡試験を行ったとき,インピーダンス電圧を1.2［kV］,インピーダンスワットは7.2kWであった。
  • 百分率インピーダンス［%］を求めよ。

%Z=IZ/E*100＝1.2/20*100＝6％

  • 百分率抵抗降下［%］を求めよ。

％ｒ＝I1r/V1*100=rI1^2/V1I1*100=7.2/1000*100=0.72%

  • 遅れ力率80%における電圧変動率［%］を求めよ。

ε＝(Vo-Vn)/Vn=I(rcosθ+xsinθ）/Vn=pcosθ+ｑsinθ

％Ｚ＝√p^2+q^2 6^2=0.72^2+q^2 q=5.96

ε＝0.72*0.8+5.96*0.6 ＝4.15％

④③において,この変圧器を一次電圧の値を変えることなく無負荷にしたときの二次電圧［V］を求めよ。

ε＝(V2o-V2n)/V2n 0.0415=V20-6600/6600 V20=6874[V]

問題６
定格容量30［kV・A］の変圧器があり,力率１における全負荷時の効率が97.8［%］,力率１における50%負荷時の効率が98.2［%］であった。

効率η＝出力[W]/入力[W]=出力[W]/（出力[W]+損失[W]) 効率η=pcosθ/（pcosθ+pi+pcn） 効率η=αpcosθ/（αpcosθ+pi+α^2pcn）・・・α：負荷率

  • 全負荷時の損失の合計値［kW］を求めよ。

効率η=pcosθ/（pcosθ+pi+pcn） 0.978＝30*1/（30*1+pi+pcn) pi+pcn=0.6748[kw]

  • 鉄損［kW］を求めよ。

効率η=αpcosθ/（αpcosθ+pi+α^2pcn）・・・α：負荷率 　　η＝30*0.5/（30*0.5+pi+0.5^2*pcn）=0.982 pi+1/4pcn=0.2749 pi=0.1416[kW] Pcn=0.5332[kW]

  • 力率１のとき,最大効率になる負荷［kW］を求めよ。

pi=α^2pcn α＝√pi/pcn=√0.1416/0.5332＝0.5153 30*0.5153*1＝15.5[kW]

  • 力率90%(遅れ),25［kV・A］の負荷時の効率［%］を求めよ。

α＝25/30＝5/6 η＝25*0.9/（25*0.9+0.1416+(5/6)^2*0.5332) ＝22.5/22.5+0.1416+0.3703＝97.8[%]

問題７
定格容量100［kV・A］,定格一次電圧6300V,定格二次電圧210Vの単相変圧器において,無負荷試験および 短絡試験を行った。 無負荷試験・・・(二)次側の回路を開放して(一)次側の回路に定格電圧を加えたところ,電力計の指示値は800［W］であった。 短絡試験・・・(二)次側の回路を短絡して(一)次側の回路にインピーダンス電圧を加え,定格電流を流したところ,電力計の指示値は1400［W］であった。 (１)文中の( )内のうち,正しい語句を選べ。 (２)一次側励磁抵抗［Ω］および巻線の一次側換算抵抗［Ω］をそれぞれ求めよ。

P1=V1^2/ｒ r=6300^2/800=49613[Ω]

Pcn=(r1+a^2r2)I^2 S=V1I1 100*10^3=6300I1 I1=15.87[A] 1400=(r1+a^2r2)*15.87^2 r1+a^2r2=5.56[Ω] (３)この変圧器を１日のうち８時間は力率0.80の定格容量で運転し,８時間は力率１で1/2の負荷で運転し,残り８時間は無負荷で運転したときの全日効率［%］を求めよ。

問題８
定格一次電圧100［V］,定格二次電圧120［V］の単相単巻変圧器がある。 無負荷で一次側に100［V］の電圧を加えたときの励磁電流は1［A］であった。 この変圧器の二次側に抵抗負荷を接続し,一次側に100Vの電源に接続して二次側に大きさ15［A］の電流が流れたとき,分路巻線の電流［A］の大きさを求めよ。 ただし,巻線の抵抗および漏 れリアクタンスならびに鉄損は無視できるものとする。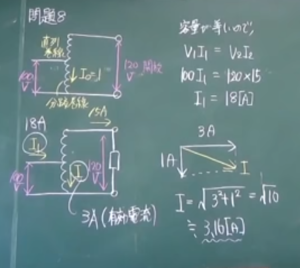  
問題９
変圧器の並行運転について,以下の問いに答えよ。 (１)２台の変圧器を並行運転させる条件として,以下の下線部に適する語句をそれぞれ答えよ。
  • 極性が同じであり, 定格電圧と  巻数比  が等しい。
この条件が満たされないと     循環    電流が流れる。
  • 百分率インピーダンスが等しい
  • 抵抗と漏れリアクタンスの比が等しい
  • 相回転と角変位が等しい
(２)以下の２台の変圧器をつかって並行運転を行い,いずれも過負荷にならないようにするときに,二次側に 加えることができる最大負荷［kV・A］はいくらか。
定格容量［kV・A］ 短絡インピーダンス［Ω］
変圧器A ３０ ５
変圧器B ２０ １０
＜おすすめ記事＞ 電験3種　機械のおすすめの勉強先リンク