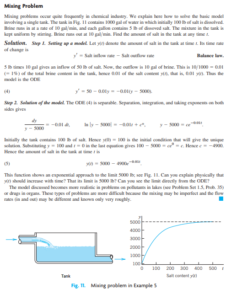
Mixing Problem

Mixing problems occur quite frequently in chemical industry. We explain here how to solve the basic model
involving a single tank. The tank in Fig. 11 contains 1000 gal of water in which initially 100 lb of salt is dissolved.
Brine runs in at a rate of 10 gal min, and each gallon contains 5 lb of dissoved salt. The mixture in the tank is
kept uniform by stirring. Brine runs out at 10 gal min. Find the amount of salt in the tank at any time t

混合の問題は、化学産業で非常に頻繁に発生します。 ここで、基本モデルを解く方法を説明します
単一のタンクを含む。 図11のタンクには1000ガロンの水が入っており、最初に100ポンドの塩が溶解します。
塩水は10ガロンの割合で流れ込み、各ガロンには5ポンドの溶解した塩が含まれています。 タンク内の混合物は
攪拌して均一に保ちました。 塩水は10 gal分でなくなります。 タンク内の塩の量をいずれのtにおいて見つける

Solution. Step 1. Setting up a model. Let denote the amount of salt in the tank at time t. Its time rate
of change is

$y^{’}= Salt inflow rate – Salt outflow rate$

 

 

 

 

 

解決。 ステップ1.モデルのセットアップ。 時間tにおけるタンク内の塩の量を示してみましょう。 その時間変化率は

$y^{’}= Salt inflow rate – Salt outflow rate$

 

5 lb times 10 gal gives an inflow of 50 lb of salt. Now, the outflow is 10 gal of brine. This is
10/1000 = 0.01(=1%) of the total brine content in the tank, hence 0.01 of the salt content y(t), that is, 0.01y(t) . Thus the
model is the ODE

$y^{‘} =50-0.01y = -0.01(y – 5000 ) $

5 lb×10 galの場合、50 lbの塩が流入します。 現在、流出は10 galのブラインです。 これは、10/1000 =タンク内の総ブライン含有量の0.01（= 1％）であるため、塩含有量y（t）の0.01、つまり0.01y（t）です。 したがって、モデルはODEです
$y^{‘} =50-0.01y = -0.01(y – 5000 ) $

Step 2. Solution of the model. The ODE (4) is separable. Separation, integration, and taking exponents on both sides gives

$\frac{dy}{y – 5000} = -0.01dt,　ln|y-5000| = -0.01t + c^{*}, y -5000 = ce^{-0.01t} $

ステップ2.モデルの解決策。 ODE（4）は分離可能です。 両側の分離、統合、および指数の取得により、
$\frac{dy}{y – 5000} = -0.01dt,　ln|y-5000| = -0.01t + c^{*}, y -5000 = ce^{-0.01t} $

Initially the tank contains 100 lb of salt. Hence y(0) = 100 is the initial condition that will give the unique
solution. Substituting y = 100 and t = 0 in the last equation gives 100 – 5000 = ce0 = c Hence c = -4900.
Hence the amount of salt in the tank at time t is

$ y(t)  = 5000 – 4900e^{-0.01t} $

最初、タンクには100ポンドの塩が含まれています。 したがって、y（0）= 100は、一意の解を与える初期条件です。 最後の式でy = 100とt = 0を代入すると、100-5000 = ce0 = cとなり、c = -4900になります。
したがって、時間tでのタンク内の塩の量は
$ y(t)  = 5000 – 4900e^{-0.01t} $

This function shows an exponential approach to the limit 5000 lb; see Fig. 11. Can you explain physically that
y(t) should increase with time? That its limit is 5000 lb? Can you see the limit directly from the ODE?
The model discussed becomes more realistic in problems on pollutants in lakes (see Problem Set 1.5, Prob. 35)
or drugs in organs. These types of problems are more difficult because the mixing may be imperfect and the flow
rates (in and out) may be different and known only very roughly.

この機能は、5000 lbの限界への指数関数的アプローチを示しています。 図11を参照してください。
y（t）は時間とともに増加しますか？ その限界は5000ポンドですか？ ODEから直接制限を確認できますか？
議論されているモデルは、湖の汚染物質に関する問題においてより現実的になります（問題セット1.5、Prob。35を参照）。
または臓器の薬。 これらのタイプの問題は、混合が不完全で、流量（流入および流出）が異なり、非常に大まかにしかわからないため、より困難です。

 

 

数学を学ぶ意義：https://livemyself.com/archives/19038

[おすすめ図書]

上記リンクから購入した方は、内容の電子データを差し上げます。
ブログ管理人に気軽にメッセージしてください。